Характеристики аддитивных помех. Сосредоточенные помехи. Импульсные помехи

Характеристики аддитивных помех

Сосредоточенные помехи

Сосредоточенными по спектру помехами называют помехи в виде синусоидального колебания, модулированного по одному или нескольким параметрам (амплитуде, частоте, фазе). Основная часть мощности таких помех сосредоточена в относительно узкой полосе частот, как правило, меньшей, чем полоса пропускания РПрУ.

Сосредоточенные помехи создаются сигналами посторонних радиостанций, а также излучениями генераторов высокой частоты различного назначения (промышленными или медицинскими). Действию сосредоточенных помех особенно подвержены каналы в диапазоне мириаметровых, километровых, гектометровых и декаметровых волн.

Это обстоятельство является следствием условий распространения радиоволн, в результате которых излучения радиопередатчиков создают заметные напряженности поля на значительных расстояниях.

При большом числе станций эти излучения складываются и образуют помеху, близкую по своим свойствам к флуктуационной.

В ряде случаев на вход РПрУ поступают отдельные сосредоточенные помехи, которые резко выделяются на общем шумовом фоне и имеют мощности, соизмеримые с полезным сигналом. Такие помехи представляют собой квазигармонические колебания (т. е. синусоидальные колебания с медленно изменяющимися амплитудами и фазами). В частном случае это может быть и синусоидальное колебание с постоянными амплитудой и фазой.

U_c(t) + U_П(t)= U_c sinw_ct+ U_Пsin(w_c+W)t= U_S sin[w_ct+q(t)]

U_S = U_c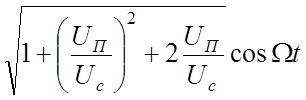

 

q(t) = arctg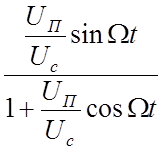

Cинусоидальная помеха изменяет сигнал как по амплитуде, так и по фазе.

При воздействии сигнала

u_c = U_c sinw_ct

и помехи

U_Пsin(w_c+W)t

суммарное колебание

	u= uc + uП= USsin [wct+q(t)]
			(1)

 

где     U_S = U_{c ,}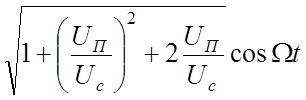

q(t) = arctg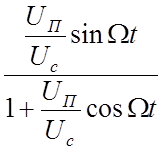

Из (1) следует, что синусоидальная помеха изменяет сигнал, как по амплитуде, так и по фазе.

Статистические свойства сосредоточенных помех описываются их распределением по частоте и по уровню. Во многих случаях можно считать распределение по частоте равномерным, а распределение уровня (квадрата амплитуд) отдельных помех во времени – логарифмически-нормальным.

р(U_П) =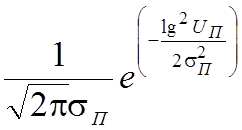

р(U_П) =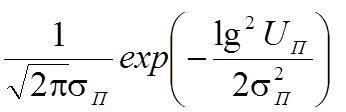

р(f) – равномерн.

Импульсные помехи

Импульсная помеха представляет собой регулярную, а чаще хаотическую последовательность кратковременных импульсов, длительность которых меньше, а интервал следования больше длительности переходных процессов в тракте РПрУ.

К таким помехам относятся многие виды атмосферных и индустриальных помех.

Одиночный импульс помехи u_П(t) можно представить в форме интеграла Фурье

u_П(t) = ,

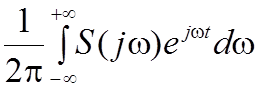где S(jw) – спектральная плотность комплексной амплитуды.

Из определения импульсной помехи следует, что импульсная помеха на входе приемника обладает более широким спектром, чем полоса пропускания РПрУ.

Типичной формой импульсных помех является апериодическая помеха, изменяющаяся по экспоненциальному закону

 

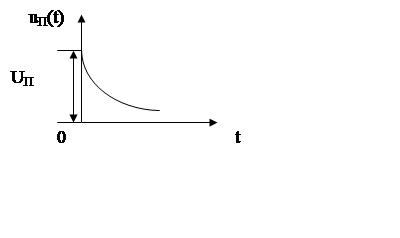u_П(t) = U_П e^-at    при t³0,

u_П(t) = 0      при t< 0.

Спектральная плотность такой помехи определяется интегралом Фурье

S(jw) =

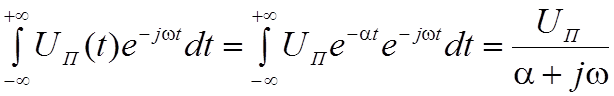
Модуль спектральной плотности амплитуды и ее фаза

S(w) =

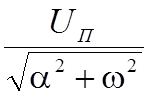
j(w) =arctg.

р(U_П) =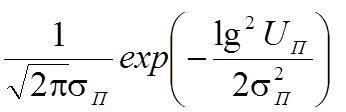

Распределение числа импульсов помехи во времени можно считать близким к распределению Пуассона

р(k) =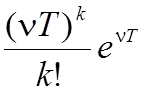

где     n – средняя частота следования импульсов.

р(k) – вероятность появления k импульсов за время Т.

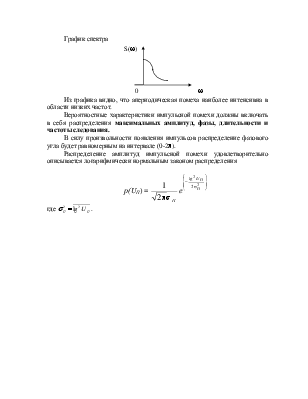
График спектра

 

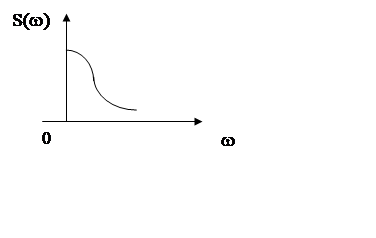Из графика видно, что апериодическая помеха наиболее интенсивна в области низких частот.

Вероятностные характеристики импульсной помехи должны включать в себя распределения максимальных амплитуд, фазы, длительности и частоты следования.

В силу произвольности появления импульсов распределение фазового угла будет равномерным на интервале (0-2p).

Распределение амплитуд импульсной помехи удовлетворительно описывается логарифмически нормальным законом распределения

р(U_П) =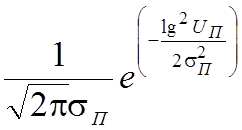

где .