Расчёт параболической зеркальной антенны с рупорным облучателем, страница 2

 – уровень облучения края зеркала ().

Диаграмма направленности рупора в плоскости E в пределах главного лепестка описывается выражением ([2], стр. 23, (44))

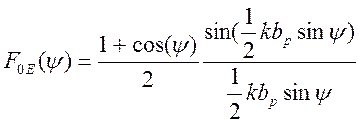  .                                  (3.8)

Таким образом, получим трансцендентное уравнение

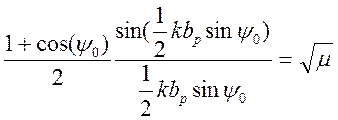                                   (3.9)

Введя обозначение

 

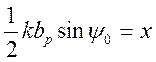
и перенося все известные величины в правую часть, получим уравнение

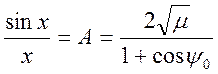.                               (3.10)

Для определенности примем дБ и выразим m в безразмерной величине.

Решим уравнение  графически относительно x, используя функцию трассировки в MathCAD (рис. 3.2).

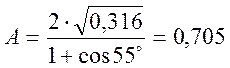
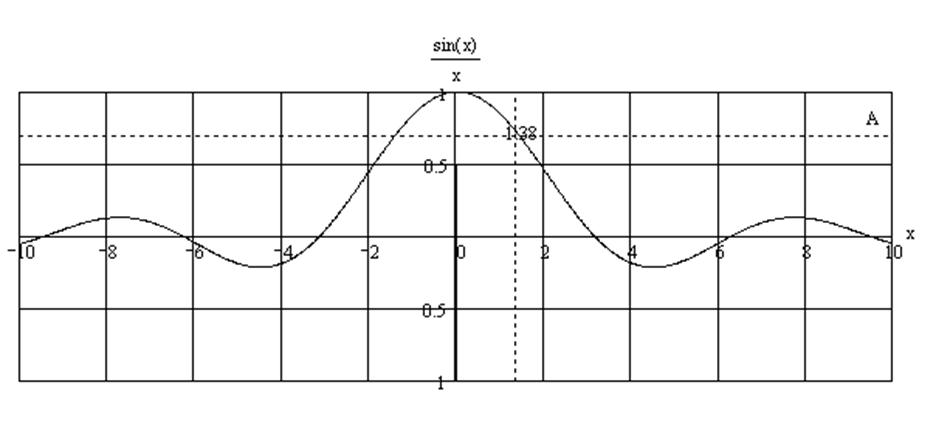Рисунок 3.2

Из графика (рис. 3.2) видно, что корнем уравнения является x₀=1,38 (отрицательный корень отбросим из физического смысла). Отсюда определим искомый размер :

,

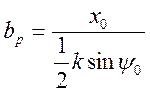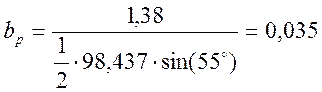 м

Диаграмма направленности рупора в плоскости H дается выражением

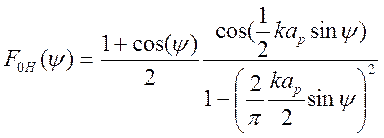                                    (3.11)

Диаграммы направленности рупора и антенны в целом ([2], стр. 8) предполагаются осесимметричными. Это требование будет удовлетворено с достаточной точностью, если обеспечить равенство уровней диаграмм в плоскостях E и H при угле y=y₀. В связи с этим нужно решить уравнение ([2], стр. 26, (50))

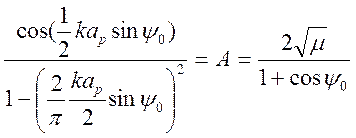                                   (3.12)

Обозначим 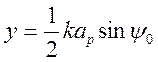 и решим уравнение (3.12) относительно y графически, используя функцию трассировки в MathCAD (рис. 3.3).

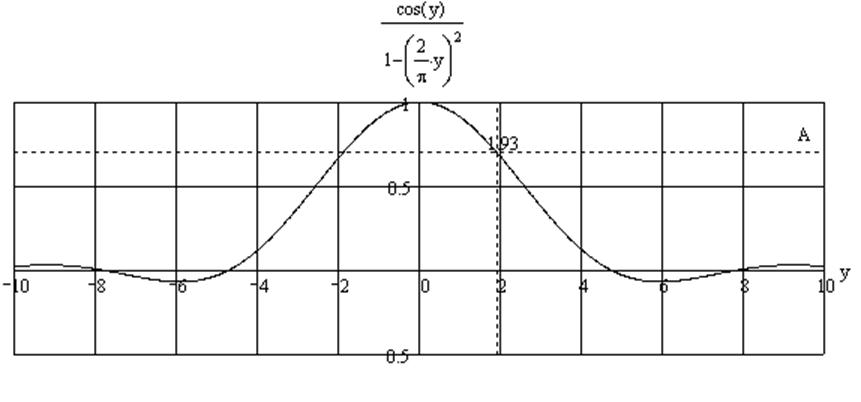
Рисунок 3.3

Из графика видно, что корнем уравнения является y₀=1,93 (отрицательный корень отбросим из физического смысла). Отсюда определим искомый размер :

,

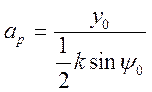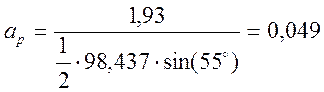 м

Исходя из условия допустимых фазовых ошибок в апертуре рупора не более 45°, рассчитаем минимальную длину рупора L ([2], стр. 26, (51))

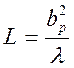                                                  (3.13)

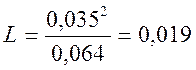 м

Зная размеры апертуры рупора, можно записать выражение для диаграммы направленности F₀(y) облучателя антенны.

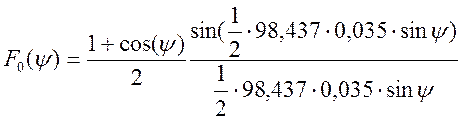
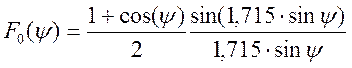                               (3.14)

Результаты расчета по формуле (3.14) приведены в таблице 3.1.

График диаграммы направленности облучателя приведен на       рисунке   3.4.

Таблица 3.1

Угол, отсчитываемый от нормали к облучателю y, град	Диаграмма направленности F0(y), безразмерная	Угол, отсчитываемый от нормали к облучателю y, град	Диаграмма направленности F0(y), безразмерная
-180	1.658e-3	10	0.979
-170	0.015	20	0.919
-160	0.040	30	0.831
-150	0.073	40	0.726
-140	0.108	50	0.619
-130	0.144	60	0.518
-120	0.179	70	0.431
-110	0.215	80	0.358
-100	0.254	90	0.301
-90	0.301	100	0.254
-80	0.358	110	0.215
-70	0.431	120	0.179
-60	0.518	130	0.144
-50	0.619	140	0.108
-40	0.726	150	0.073
-30	0.831	160	0.040
-20	0.919	170	0.015
-10	0.979	180	1.658e-3
0	1.000

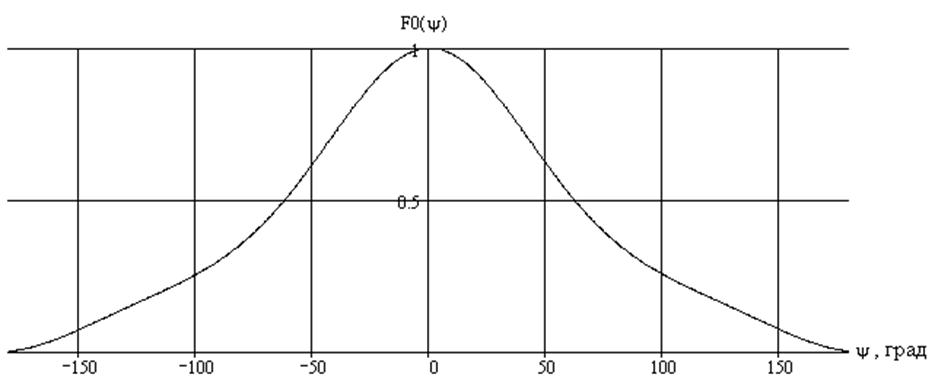
Рисунок 3.4

После отражения от зеркала сферическая волна, исходящая от облучателя, трансформируется в плоскую волну в апертуре зеркала диаметром 2R. Распределение электрического поля этой волны в апертуре (E_s) обладает симметрией относительно центра апертуры, то есть поле зависит только от координаты r. Апертурное распределение поля  связано с диаграммой направленности облучателя соотношением ([2], стр. 11, (21))

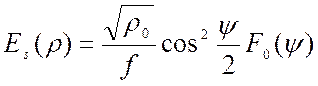,                                   (3.15)

где

r₀=120p – волновое сопротивление свободного пространства,

Связь между координатами y и rдается выражением ([2],стр. 11, (22))

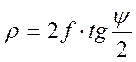.                                        (3.16)

В [2] приведено выражение для диаграммы направленности апертурного поля по мощности (стр. 9, (16)). Чтобы получить диаграмму направленности по полю, вычислим квадратный корень из правой и левой частей. Тогда диаграмма направленности по полю выражается через E_s(r) следующим образом

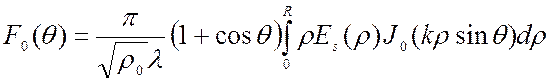,                     (3.17)

где

J₀(×) – функция Бесселя нулевого порядка.

Нормируем полученную функцию и запишем.

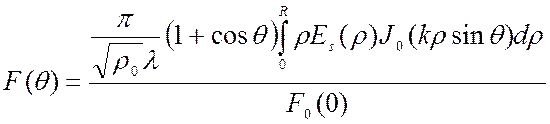                       (3.18)

Диаграмму направленности апертурного поля в логарифмическом масштабе определим по формуле

.                                                (3.19)

Результаты расчета на ЭВМ по формулам (3.18) и (3.19) приведены в таблице 3.2.

Таблица 3.2

Угол, отсчитываемый от нормали к облучателю по направлению от зеркала q, град	Диаграмма направленности апертурного поля F(q), безразмерная	Диаграмма направленности апертурного поля в логарифмическом масштабе FdB(q), дБ
-180	9.880e-4	-60.105
-175	5.575e-5	-85.075
-170	7.025e-4	-63.067
-165	1.190e-3	-58.490
-160	3.949e-4	-68.071
-155	1.165e-3	-58.675
-150	1.422e-3	-56.944
-145	6.227e-4	-64.115
-140	1.910e-3	-54.381
-135	6.341e-4	-63.957
-130	2.036e-3	-53.823
-125	1.806e-3	-54.865
-120	6.888e-4	-63.239
-115	2.647e-3	-51.547
-110	2.918e-3	-50.698
-105	2.081e-3	-53.634
-100	1.055e-3	-59.535
-95	4.129e-4	-67.683
-90	4.336e-4	-67.258
-85	1.312e-3	-57.642
-80	3.117e-3	-50.125
-75	5.285e-3	-45.539
-70	5.872e-3	-44.625
-65	2.086e-3	-53.613
-60	5.532e-3	-45.143
-55	8.224e-3	-41.698
-50	2.517e-3	-51.982
-45	0.012	-38.407
-40	4.035e-3	-47.883
-35	0.016	-36.011
-30	0.016	-35.899
-25	0.011	-39.340
-20	0.041	-27.713
-15	0.039	-28.171
-10	4.502e-3	-46.933
-5	0.565	-4.962
0	1.000	0.000
5	0.565	-4.962
10	4.502e-3	-46.933
15	0.039	-28.171
20	0.041	-27.713
25	0.011	-39.340
30	0.016	-35.899
35	0.016	-36.011
40	4.035e-3	-47.883
45	0.012	-38.407
50	2.517e-3	-51.982
55	8.224e-3	-41.698
60	5.532e-3	-45.143
65	2.086e-3	-53.613
70	5.872e-3	-44.625
75	5.285e-3	-45.539
80	3.117e-3	-50.125
85	1.312e-3	-57.642
90	4.336e-4	-67.258
95	4.129e-4	-67.683
100	1.055e-3	-59.535
105	2.081e-3	-53.634
110	2.918e-3	-50.698
115	2.647e-3	-51.547
120	6.888e-4	-63.239
125	1.806e-3	-54.865
130	2.036e-3	-53.823
135	6.341e-4	-63.957
140	1.910e-3	-54.381
145	6.227e-4	-64.115
150	1.422e-3	-56.944
155	1.165e-3	-58.675
160	3.949e-4	-68.071
165	1.190e-3	-58.490
170	7.025e-4	-63.067
175	5.575e-5	-85.075
180	9.880e-4	-60.105