Метод получения наноалмазов, основанный на использовании СВЧ газового разряда низкого давления в магнитном поле, является альтернативой детонационному методу .
Осаждение углеродных пленок осуществляется в плазме паров этанола в СВЧ газовом разряде на стеклянную подложку в специальной установке. Но пока данный метод не до конца изучен.
3. Физическая природа наноалмазного состояния
3.1 Алмазная квантовая точка
На поверхности природного алмаза колебательная энергия поверхностных состояний по данным спектроскопии характеристических потерь энергии электронов высокого разрешения (HREELS) изменяется в диапазоне 50-400 мэВ в зависимости от состояния поверхности при гидрировании . Примерно в этом же диапазоне энергий наблюдаются изменения частот в ИК спектре, когда проводимость NDC изменяется на 12 порядков в зависимости от соотношения ND и пироуглерода . Если предположить, что NDS является универсальным и имеет одинаковую природу в ND, NDC и на поверхности монокристаллов алмаза, то, используя идею Тамма, легко определить, что длины электронных волн де Бройля l лежат в диапазоне ~ 2-5 nm (Рис. 1). Данное предположение лежит в основе модели алмазной квантовой точки (DQD).
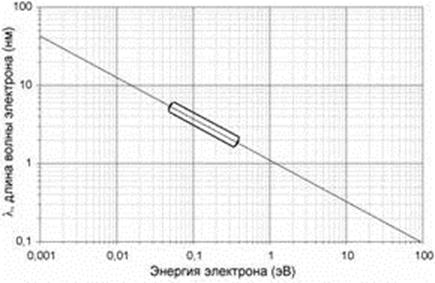
Рис.1. Зависимость длины волны де Бройля от энергии электрона hn. E, p; n=E/h; l=h/p; p=mec; h=6,6748×10-27 эрг×с. Выделена область термодинамической устойчивости наноалмаза.
Эти же значения характеризуют "окно" термодинамической стабильности ND. Расчетами ab initio определена стандартная теплота образования нано фаз углерода и показано, что ND - не обязательно самая устойчивая фаза в нано масштабе, но "окно" стабильности находится между ~1.9 и ~5.2 nm. Т.е. наноалмаз термодинамически устойчивее других форм углерода, если содержит от ~1,1*103 до ~2,5*104 атомов . Так как резонансные с самосогласованным полем излучения колебательные структуры связаны с колебаниями электронной плотности (волны де Бройля), то надо включить энергию в определение квантовой точки.
Алмазной квантовой точкой с колебательной энергией hn будем называть частицу преимущественно с sp3 гибридизацией, размер которой порядка длины волны де Бройля с энергии hn.
3.2 Описание поверхности алмаза
Электронно-колебательные состояния на поверхности природного алмаза исследованы очень хорошо, что помогает понять природу NDS в силу его универсальности. Спектроскопия характеристических потерь энергии электронов высокого разрешения (HREELS) позволяет определять энергии поверхностных колебательных состояний, которые существенно изменяются в диапазоне 50-400 мэВ в зависимости от состояния поверхности .
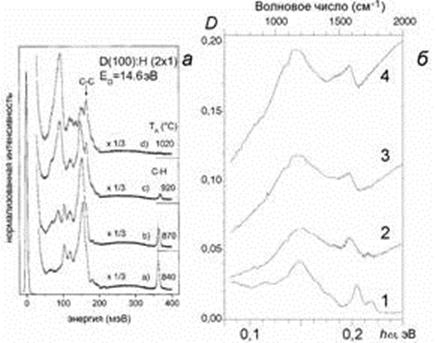
Рис.2. а) HREELS поверхности природного алмаза. Заимствовано из работы . б) FTIR спектры пористого полупроводника из ND при различной проводимости (см. табл.1), зависящей от доли пироуглерода g: (1) g = 0; (2) g = 10; (3) g = 20; (4) g = 30. Из работы .
Механизм поверхностной проводимости алмаза не выяснен [53]. Удивительно, что углерода нет в последнем обзоре по квантовым точкам [54], хотя баллистическая проводимость по поверхностным состояниям Тамма и Шокли хорошо изучена [55, 56]. Резонансные с полем излучения колебательные структуры связаны с колебаниями электронной плотности.
3.3 Полупроводник из алмазных квантовых точек
Рассмотрим проводимость пористого полупроводника из алмазных квантовых точек. Зависимость объемной проводимости нанокомпозитов от температуры показана на рис.6 и имеет типичный для полупроводников вид. Из температурных зависимостей электропроводности следует аналогия нанокомпозита с узкозонными аморфными полупроводниками. Однако к рассматриваемому случаю вместо обычных валентной зоны и зоны проводимости применимо представление Пекара об одномерной и двумерной зонах поверхностных электронных состояний. Степень заполнения этих состояний, их взаимное расположение на энергетической шкале и разность энергий между ними трудно определить из данных по температурной зависимости объемной проводимости NDC на постоянном токе.
В нанокомпозите нет газа свободных электронов, как в сплошных металлах и полупроводниках. Поэтому можно предполагать, что уровень Ферми находится в середине запрещенной зоны между одномерной и двумерной зонами поверхностных электронных состояний. Электроны в пределах каждой частицы слабо локализованы в ней, т.к. длина волны де Бройля порядка размера частиц алмаза (Рис.1). Энергии активации прыжковой проводимости нанокомпозита, определенные из зависимости s(T) (рис.3), составляют величины от 0.03 до 0.3 эВ (табл.1). Объемная проводимость при низких температурах описывается формулой Мотта для амофных полупроводников [76], что видно на врезке рис.6, где в координатах lg σ = f(T-1/4) линейность наблюдается от 200 до 4 K.
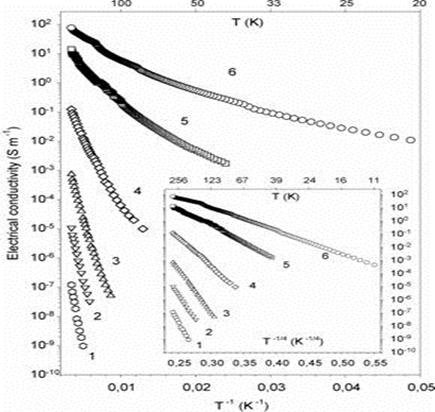
Рис.3. Температурные зависимости проводимости полупроводника из алмазных квантовых точек при разных долях пироуглерода g: (1) g = 0.5; (2) g = 5; (3) g = 10; (4) g = 20; (5) g = 30; (6) g = 40. Из работы .
Изменение объемной электрической проводимости на 12 порядков при изменении γ от 0 до 0.5 невольно заставляет думать не столько о прямой аналогии NDC с переходом металл-диэлектрик, сколько о физике самого явления.
|
Образец |
γ, % |
Термоэдс, μV/K |
|
NDC20 #В4 |
17,4 |
6.6 0.2 |
|
NDC20 #В3 |
19 |
6.5 0.6 |
|
NDC30 #Q |
29,5 |
5.6 0.1 |
|
NDC30 #P = #Q - δ |
29,5 |
6.3 0.2 |
Таблица 2. Термоэдс NDC
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.