где S — полная излучающая поверхность нагревателя, м2; температуры Тс и Тж измеряются в Кельвинах; степень черноты поверхности ε = 0,35.
Для Р1: Рлуч = 5,67·0,35·0,22·0,115·[(301/100)4 – (296/100)4] = 0,267 Вт.
Р1 = Рэл – Рлуч = 0,52 – 0,267 = 0,253 Вт.
α1 = Р1/[(Тс – Тж)·S] = 0.133/[(301–296)·0,22·0,115] = 2 Вт/К·м2.
Для Р2: Рлуч = 5,67·0,35·0,22·0,115·[(302/100)4 – (296/100)4] = 0,322 Вт.
Р2 = Рэл – Рлуч = 0,725 – 0,314 = 0,403 Вт.
α2 = Р1/[(Тс – Тж)·S] = 0.646/[(302–296)·0,22·0,115] = 2,72288 Вт/К·м2.
Для Р3: Рлуч = 5,67·0,35·0,22·0,115·[(311,6/100)4 – (296/100)4] = 0,879 Вт.
Р3 = Рэл – Рлуч = 2,8 – 0,879 = 1,921 Вт.
α3 = Р1/[(Тс – Тж)·S] = 1,921/[(311,6–296)·0,22·0,115] = 4,86723 Вт/К·м2.
3. Таким образом, каждому экспериментальному значению мощности Рэлi поставлены в соответствие Рi, αi, Tci, т.е. опытные данные подготовлены к нахождению критериальной зависимости вида
Nu = f(Pr, Gr) (4).
Поскольку данное уравнение в качестве независимых переменных содержит комплексы Nu, Pr, Gr, именно их и следует вычислить для каждого i по полученным αi и Tci. Однако предварительно рассмотрим следующее.
Во-первых, комплексы Nu, Pr, Gr, содержат зависящие от температуры теплофизические параметры жидкости ν, α, β, λ. Так как в любом эксперименте температура жидкости плавно изменяется от Тс непосредственно у поверхности до Тж на значительном удалении, перечисленные параметры также не остатся постоянными. Введем так называемую «определяющую температуру»
Tm = (Tc + Tж)/2 (5).
Значение теплофизических параметров, отвечающие температуре Тm, являются средними для приповерхностного слоя жидкости. Их принято снабжать индексом m. Очевидно, что для учета неоднородности приповерхностного слоя критерии Nu, Pr, Grследует вычислять по значениям νm, αm, βm, λm.
Во-вторых, в качестве размера l, входящего в критерии Nuи Gr, при полном подобии в принципе может быть взят любой размер тела. Однако, если в качестве l принять тот размер, в направлении которого развиваются конвективные потоки, то полученные из экспериментов уравнения (4) оказываются более универсальными, так как требование геометрического подобия при этом может быть снято. Такой характерный размер называется определяющим и обозначается L. В случае свободной конвекции для вертикальных поверхностей определяющим размером является высота, для горизонтальных цилиндров и шаров — диаметр, для горизонтальных плоскостей — меньший из двух размеров. При этом вид уравнения (4) будет одинаков, но под L в каждом случае будет подразумеваться различная величина.
Таким образом, поиск вида зависимости (4) нужно начинать с установления определяющего размера L для экспериментального объекта и нахождения определяющей температуры Tm. Далее, для каждой экспериментальной точки: αi, Тсi – необходимо вычислить значения критериев подобия:
Num =αL/λm — критерий Нуссельта, его величина показывает соотношение чисто кондуктивного сопротивления жидкости и истинного конвективного в рассматриваемой группе подобных явлений.
Prm = νm/am — критерий Прандтля, характеризует соотношение скоростей распространения механических и тепловых возмущений в жидкости и является её теплофизической характеристикой.
Grm = βmgΔTL3/νm2 — критерий Грасгофа, показывает соотношение подъёмной архимедовой силы, вызывающей свободную конвекцию, и сил вязкости, препятствующих движению.
ΔT = Тс – Тж, βm = 1/Тm.
Для Р1: λm = 2.49·10-2 Вт/К·м; am = 21.37·10-6 м2/с; νm = 14,93·10-6 м2/с.
Tm = (296+301)/2 = 298,5 K
Num = 2·0.22/2.63·10-2 = 16,73
Prm = 14,93·10-6/22,15·10-6 = 0.674
Grm = 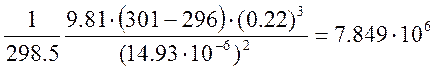
Для Р2: λm = 2.57·10-2 Вт/К·м; am = 22.02·10-6 м2/с; νm = 15,38·10-6 м2/с.
Tm = (296+301.85)/2 = 298,93 K
Num = 2.723·0.22/2.57·10-2 = 23,3
Prm = 15,38·10-6/22,02·10-6 = 0.698
Grm = 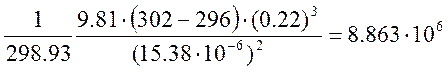
Для Р3: λm = 2, 66·10-2 Вт/К·м; am = 23,45·10-6 м2/с; νm = 16,366·10-6 м2/с.
Tm = (296+311.6)/2 = 303,8 K
Num = 4,86·0.22/2.66·10-2 = 40,2
Prm = 16,366·10-6/23,45·10-6 = 0.697
Grm = 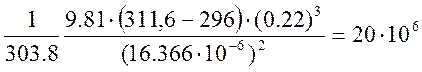
4. Теперь для всех I экспериментальных точек получены определяющие критерии Prmи Grm и определяемый Num. В силу плавности кривых, характеризующих конвективный теплообмен, критериальное уравнение (4) при свободной конвекции принято записывать в виде
![]() (6)
(6)
Следовательно, для конкретизации уравнения (6) по экспериментальным данным необходимо определить коэффициент С и показатель степени n. Для этого нужно прологарифмировать произведение (Pr·Gr)mи Num, поскольку в логарифмических координатах (6) обращается в прямую линию:
![]() (7)
(7)
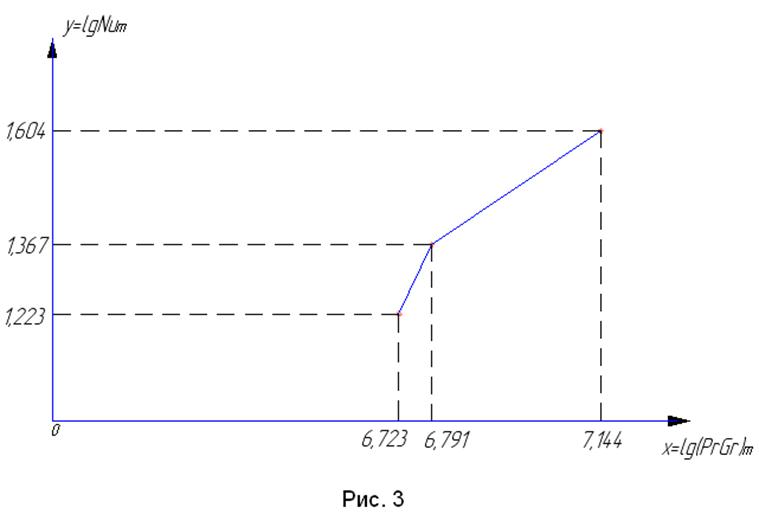
Для Р1 = 0,52 Вт: lgNum = 1,223, lg(Pr·Gr)m = lg(5290226) = 6,72347
Для Р2 = 0,725 Вт: lgNum = 1,367, lg(Pr·Gr)m = lg(6186374) = 6,79144
Для Р1 = 2,8 Вт: lgNum = 1.604, lg(Pr·Gr)m = lg(13940000) = 7,144
Обозначим x = lg(Pr·Gr)m, y = lgNum, a=lgC. На рис. 1 показан графический метод отыскания показателя степени n(n=tgφ) и постоянной А (A=y(x=0)).
Для получения коэффициента C в критериальном уравнении (4) нужно потенцировать найденное значение А (С=10А). Теперь С и n в (4) известны, так что получено критериальное уравнение, аппроксимирующее экспериментальные результаты.
Если все экспериментальные точки графика не ложатся на одну прямую и явно прослеживается нелинейность, аппроксимацию производят кусочно, т.е. кривую заменяют ломаной. При этом для отдельных участков значения С и n будут различны.
|
λm, х10-2 Вт/К·м |
νm, х10-6 м2/с |
am,х 10-6 м2/с |
|
2.49 |
14,93 |
21.37 |
|
2.57 |
15,38 |
22.02 |
|
2, 66 |
16,366 |
23,45 |
|
lg(Pr·Gr)m |
C |
n |
|
|
от |
до |
||
|
0 |
6,706 |
16,71 |
0 |
|
6,723 |
6,791 |
0,005 |
2,117 |
|
6,691 |
7,144 |
0,068 |
0,671 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
1 |
0,52 |
0,267 |
0,253 |
28 |
2 |
298,5 |
5 |
5290226 |
6,72347 |
1,223 |
|
2 |
0,725 |
0,322 |
0,403 |
29 |
2,723 |
298,93 |
6 |
6186374 |
6,79144 |
1,367 |
|
3 |
2,8 |
0,879 |
1,921 |
38,6 |
4,867 |
303,8 |
15,6 |
13940000 |
7,144 |
1.604 |
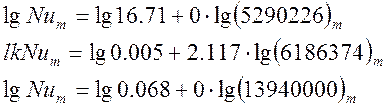
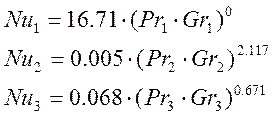
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.