Режимы систем электроснабжения. Расчёт нормального установившегося режима. Сведения о матрицах. Действия с матрицами

Математические задачи, решаемые специалистами по электроснабжению, очень разнообразны. Вот лишь некоторые из них:

1.  Расчёт установившегося симметричного режима. Эта задача решается с использованием алгебры матриц.

2.  Отыскание оптимального режима.  Эти задачи решаются методом математического программирования.

3.  Расчёт несимметричных режимов. Здесь  используется метод симметричных составляющих.

4.  Расчёт переходных процессов. Эта задача решается путём интегрирования систем обыкновенных дифференциальных уравнений.

5.  Исследование устойчивости. Эти задачи решаются путём анализа дифференциальных уравнений по некоторым критериям.

6.  Вопросы прогнозирования нагрузок, оценка надёжности и аварийности. Эти задачи решаются с использованием методов теории вероятности и математической статистики.

7.  Расчёт несинусоидальных режимов. Здесь используются методы спектрального анализа

Режимы СЭС

Режим системы – состояние системы в некоторый момент времени или на интервале времени.

Параметры режима – токи, напряжения, мощности, эдс.

Параметры системы – сопротивления, коэффициенты трансформации, постоянные времени.При анализе и составлении математического описания различают три основных режима СЭС:

1.  Нормальный установившийся режим, применительно к которому проектируется электрическая система.

2.  Послеаварийный установившийся режим, наступающий после аварийного отключения какого-либо элемента системы. Как нормальный, так и послеаварийный установившиеся режимы характеризуются параметрами, не изменяющимися во времени. При этом связи между параметрами режима представляются алгебраическими уравнениями.

3.  Переходный режим, во время которого система переходит от одного состояния к другому. Для него характерно изменение его параметров во времени и описание его дифференциальными уравнениями.

Расчёт нормального установившегося режима

Расчёт установившегося режима СЭС выполняют на стадии проектирования и в процессе эксплуатации.

Расчёт установившегося режима позволяет:

1.  Правильно выбрать конфигурацию схемы, для которой токи и напряжения в её элементах находятся в заданных пределах.

2.  Определить наиболее экономичный режим работы.

Исходными данными для расчёта являются:

1.  Схема замещения СЭС.

2.  Токи, напряжения или мощности источников электроэнергии.

3.  Токи, сопротивления или мощности потребителей электроэнергии (нагрузок).

4.  Сопротивления или проводимости элементов СЭС.

Целью расчёта является нахождение токов, напряжений, мощностей в элементах СЭС.

Сведения о матрицах

Матрицы позволяют представить решение систем уравнений в компактной форме, а также построить алгоритм для решения на компьютерах.

Матрицей называется таблица величин, записанных в определённой последовательности.

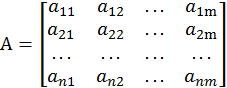
Элемент матрицы обозначается символом с индексом строки и столбца.

Матрица- прямоугольная и имеет размерность.

Матрица, количество строк и столбцов которой одинаково и равно, называется квадратной матрицей порядка.

Матрицы могут состоять из одного столбца (матрица-столбец) или из одной строки (матрица-строка).

Квадратная матрица, все элементы которой вне главной диагонали равны нулю, называется  диагональной

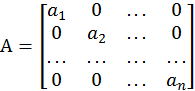или

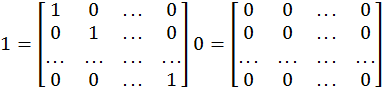
Если в диагональной матрице , то имеем единичную матрицу- го порядка, а матрица, состоящая из нулей, называется нулевой матрицей

В электротехнике используется столбцовая матрицаи строковая, состоящие из единиц:

,

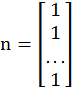Если комплексная матрица с элементами , то матрица  того же размера с элементаминазывается комплексно-сопряженной с и обозначается.

Действия с матрицами

1. Сложение матриц. Сложение двух матриц допустимо при их одинаковой размерности.

Элементматрицыопределяется как сумма элементовина одинаковых местах:.

Операция вычитания может рассматриваться как операция сложения с обратным знаком.

2. Умножение матрицы на число. Произведением матрицы на число - это матрица, полученная умножением всех элементов на это число.

3. Умножение матриц. Произведение двух матриц определено, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицыразмерана матрицуразмеромявляется матрицаразмера, элементкоторой равен сумме произведений элементов-ой строки матрицына соответствующие элементы-ого столбца матрицы:

4. Транспонирование матрицы. Преобразование матрицы, состоящее в замене строк столбцами (или столбцов строками) при сохранении их нумерации, называется транспонированием.

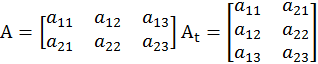
Произвольная-матрица при транспонировании становится -матрицей.

5. Обращение матрицы. Эта операция применима только к квадратным матрицам.Обратная матрицапри умножении справа или слева на заданную матрицудаёт единичную матрицу:

Обратная матрица существует для матрицы, если её определитель не равен 0:.Квадратные матрицы, определитель которых равен нулю, называются особенными. К особенным относятся:

- нулевая матрица

- матрица, суммы элементов которой по всем строкам или по всем столбцам равны нулю

- матрица, у которой есть строка из нулей или столбец из нулей.

Свойства  действий с матрицами

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10.  Если, то

Матричная запись системы линейных уравнений

Рассмотрим систему линейных уравнений

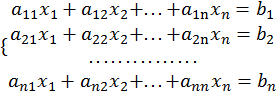
В матричной форме эта система запишется так:

где - квадратная матрица -ого порядка, называемая матрицей системы:

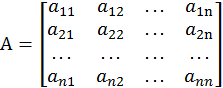
аи– матрицы-столбцы неизвестных переменных и свободных членов

      

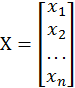
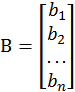
Матричное уравнение решается умножением обеих его частей слева на обратную матрицу:

В результате получаем

Блочные матрицы

Пусть матрицыиразбиты на блоки:

Если число столбцов подматрициравно числу строк подматрицы и число столбцов подматрициравно числу строк подматрицы, то истинно равенство

Разбиение на блоки позволяет выполнять операции с матрицами меньших размеров.

Минимальные сведения по языку SciLab

1.Стирание содержимого командного окна:  clc

2. Удаление всех переменных из памяти:  clear

3. Целая часть числа отделяется от дробной части точкой:    2.5

4. Мнимая единица: %i

5. Пример записи комплексного числа 6+2i :     6+%i*2

6. Квадратный корень из x:    sqrt(x)

7. Модуль вещественного или комплексного числа x:   abs(x)

8. Пример создания столбца J:  J=[ 1

2

                             -3]

9. Пример создания матрицы Z:  Z =[  1   2   3       

                               9   -8   7       

                              -10  15  20]

10. Получение матрицы M горизонтальным склеиванием матриц: M=[M1 M2]

11. Получение матрицы Dвертикальным склеиванием матриц:  D=[D1   

D2]

12. Создание диагональной матрицы     diag([10 20 30 40])

13. Создание единичной матрицы 5-го порядка:eye(5,5)

14. Создание нулевой матрицы размером 4´5: zeros(4,5)

15. Вычисление определителя  матрицы  A:   det(A)

16. Обращение матрицы A:inv(A)

17. Получение из матрицы M транспонированной матрицы :M.’

18. Взятие 5 элемента из строки или столбца U :    U(5) 

19. Взятие элемента матрицы M, стоящего на 3 строке и 2 столбце:    M(3,2)

20. Взятие части строки или столбца U с 1 по 5 элемент:   U(1:5)

21. Взятие части матрицы  M с 3 по 7 строку и с 1 по 5 столбец: M(3:7,1:5)

22. Матричное умножение матриц  Mи  I:M*I

23. Поэлементное умножение матриц A и B:     A.*B

24. Поэлементное деление матриц A и B:     A./B

25. Получение комплексно-сопряжённой к матрице или числу J:  conj(J)

26. Нахождение суммы элементов матрицы S:sum(S)

27. Задание цикла, повторяющегося 7 раз  fork=1:7       

                                                                         ........

end