Электротехника \ Теоретические основы электротехники

Исследование распределения напряженности магнитного поля вдоль оси цилиндрической катушки с электрическим током, страница 2

          Определение намагничивающей силы вдоль пути, проходящего вне катушки между точками, лежащими на концах сердечника:

          В числовом выражении


Определение намагничивающей  силы по замкнутому контуру:

В числовом выражении:

Аналогично проводим расчет для случая алюминиевого сердечника Определение намагничивающей силы вдоль пути, проходящего внутри сердечника, между точками, лежащими на концах сердечника:

 В числовом выражении:

Определение намагничивающей силы вдоль пути, проходящего вне катушки между точками, лежащими на концах сердечника:

В числовом выражении:

Определение намагничивающей силы по замкнутому контуру:

В числовом выражении:

Расчет относительной магнитной проницаемости      стального сердечника, используя показания амперметра, вольтметра, ваттметра и данными эксперимента таблицы 4 Расчет относительной магнитной проницаемости проводим по формуле:

(6)

где          - экспериментальное значение напряженности магнитного поля в точке х = О,

           при наличии магнитного сердечника (из таблицы 3) Таким образом, получаем:

Рассчитаем значения падений магнитных напряжений F1, F2, F2c,F2c  Расчет проводим следующим образом:

Для приближенного расчета сведем многослойную катушки к однослойной со средним радиусом обмотки:

(7) В числовом выражении имеем:

Падение магнитного напряжения F1 вдоль пути, проходящего внутри воздушной катушки определяем по формуле:

(8)


В числовом выражении получаем:

На основе закона полного тока и соотношения                                можем определить

действующее значение падения магнитного напряжения F2 вдоль пути , проходящего вне катушки:

(9)

В числовом выражении, получаем:

Переходим к определению расчетных падений магнитного напряжения в стальном сердечнике

Расчет проводим на основе магнитных цепей, представленных на рис. 3


а)                                                  б)

Рис.3 Магнитные цепи катушки с сердечником:

а) Для случая с магнитным сердечником;

б) Для случая с немагнитным сердечником

Используем магнитную цепь катушки с магнитным сердечником (рис. 3, б). Принимаем следующие обозначения:

-  падения магнитных напряжений, соответственно, во внутренней области
катушки и во внешней области катушки;

-  магнитные сопротивления внешней воздушной среды (по которой
происходит замыкание полного магнитного потока катушки), соответственно, без
магнитного сердечника и с магнитным сердечником;

-  магнитное сопротивление области, занимаемой стальным сердечником;

-  магнитное сопротивление воздушной полости катушки;

-  магнитное сопротивление воздушной полости сердечника.

При наличии магнитного сердечника распределение магнитного поля вдоль оси катушки можно принять равномерным, тогда магнитные сопротивления стального сердечника и внутренних областей катушки находятся по формулам:

(10)

(11)

(12)

где                        - площади поперечных сечений внутренней области катушки

сердечника и его воздушной полости соответственно.

Величины этих площадей рассчитываются по формулам:

(13) (14)


(15)

В числовом выражении получаем:

Следовательно, можем рассчитать числовые значения магнитных сопротивлений:

Далее определим магнитное сопротивление внешней воздушной среды       при отсутствии магнитного сердечника в катушке:

(13)

где                  - магнитный поток на торцевой границе катушки.

Распределение осевого магнитного поля в поперечном направлении (вдоль радиуса) в полости катушки равномерно, тогда магнитный поток в воздушной катушке определяется формулой:

Здесь              - площадь поперечного сечения катушки. Определим ее числовое

значение:

Граничное значение напряженности магнитного поля       определяется следующим образом:

(14) Подставляя (9) и (14) в (13), получаем:

(15) В числовом выражении

Используя схему магнитной цепи рис. 2, имеем:                               . Выражая

из последнего соотношения магнитный поток                                                                                                            получаем формулу

усредненного значения магнитного потока, выходящего из торца катушки:


Этот поток, действуя на магнитное сопротивление воздушной среды, окружающей катушку, вызывает падение магнитного напряжения на этом участке магнитной цепи, равное:

Очевидно,

(16)

есть магнитное сопротивление внешней воздушной среды при неоднородном распределении индукций магнитного поля в плоскости торца катушки. В числовом выражении, получаем:

При наличии ферромагнитного сердечника выполняется соотношение                                                                                                              В этом

случае                     , тогда влиянием воздушной полости осевого канала сердечника

пренебрегаем на магнитный режим катушки. Магнитная цепь упрощается, и закон полного тока сводится к следующему выражению

                                                                                                        (17)                                                                                                            Отсюда величина         определяется следующим образом:

                                                                                                            (18)                                                                                                                                    В числовом выражении:

Таким образом, определяем падения магнитных напряжений по формулам:

(19)

В числовом выражении, получаем

Экспериментальные кривые находятся в приложении 1.

ВЫВОДЫ:

Было осуществлено лабораторное исследование многослойной цилиндрической катушки, заключающееся в измерение падения магнитного напряжения при помощи магнитного пояса (по замкнутому контуру; вдоль пути, проходящего внутри сердечника, между точками, лежащими на концах сердечника; вдоль пути, проходящего вне катушки между точками, лежащими на концах сердечника), а также в измерении напряженности поля исследуемой катушки, начиная от середины катушки, и кончая на расстоянии Z/2 от катушки за пределами.

1. При изменении напряженности магнитного поля со стальным сердечником наблюдается скачок при 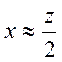.Это объясняется из граничных условий:

Граница раздела “сталь-воздух”

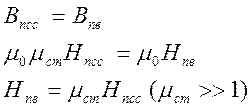
Из второго граничного условия:

Отсюда >>

2. Значительное уменьшение величины  H(x=0) в стальном сердечнике относительно случая, когда сердечник немагнитный объясняется следующим образом:

3. Перераспределение падений магнитного напряжения  и для различных сердечников объясняется исходя из анализа магнитных цепей катушки с сердечником (магнитным и немагнитным) В случае магнитного сердечника магнитное сопротивление внутри катушки меньше, чем в случае немагнитного сердечника, т.к. сопротивление стального сердечника в воздушной полости сердечника параллельны друг другу и магнитное сопротивление этого участка меньше самого малого сопротивления и падение магнитного напряжения      будет меньше, чем      на участке с сопротивлением.                  При этом                                                                                                                                 <                                                                                                                                   =IW-                                                                                                                                 = IW-                                                                                                                                                      Тогда >

Скачать файл