4.оценка систематических погрешностей процесса измерений. методы обнаружения. введение поправок. 1)метод замещения-используется идеальная мерка : I1=I2, Θ=Rобр-Rк
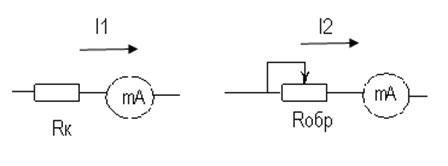
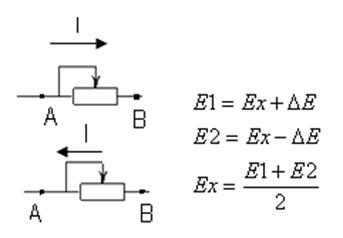
2)м-д противопоставления:исп-ют
одинарный мост,ктр регулируют ч/з R1,затем меняют плечи местами.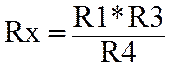 ,
, 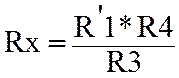 и
получаем
и
получаем 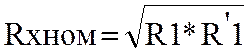 , Θ=Rх-Rхном.3)м-д
рандомизации:одну и ту же вел-ну измеряют разными методами и приборами.и чем
больше приборов и методов,тем выше вероятность,что постоянная систематическая
погрешность скомпенсируется.4)м-д компенсации по знаку-изменяют полярность ЭДС:
, Θ=Rх-Rхном.3)м-д
рандомизации:одну и ту же вел-ну измеряют разными методами и приборами.и чем
больше приборов и методов,тем выше вероятность,что постоянная систематическая
погрешность скомпенсируется.4)м-д компенсации по знаку-изменяют полярность ЭДС:
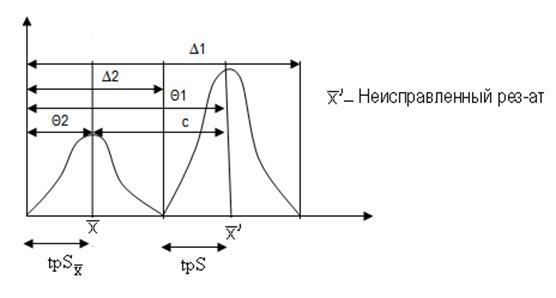
Статический метод(Критерий
Аббе)-сравнение дисперсий рез-ов измерения, найденных 2-мя путями:1)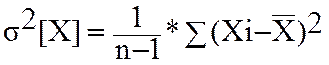 -квадрат СКО; 2)
-квадрат СКО; 2)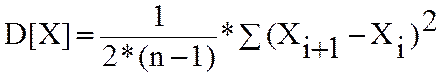 -дисперсия,хар-ет степень рассеяния
от мат.ожидания.
-дисперсия,хар-ет степень рассеяния
от мат.ожидания.![]()
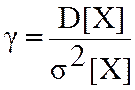 -критерии
Аббе.т.е.,присутствие сист погр приведет к смещению центра группировки
-критерии
Аббе.т.е.,присутствие сист погр приведет к смещению центра группировки ![]() .если
.если ![]() <
<![]() табличная,то сист.погр-ти нет. методы
борьбы -введение поправок-вел-на,одноименная измеряемой,ктр вводится в рез-ат
измерения для устранения сист.погр-ти.
табличная,то сист.погр-ти нет. методы
борьбы -введение поправок-вел-на,одноименная измеряемой,ктр вводится в рез-ат
измерения для устранения сист.погр-ти.![]() .
до введения поправки:∆1=Θ1+tpS; после введения попраки:∆2=Θ2+tpSx=
.
до введения поправки:∆1=Θ1+tpS; после введения попраки:∆2=Θ2+tpSx=
Θ1-c+tp*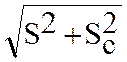 ,∆1>∆2;
,∆1>∆2; 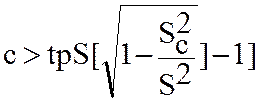 -предел введения поправок.
-предел введения поправок.
![]() 5.Оценка случайных
погрешностей измерений.основные законы распределения случ.погрешностей.при
оценке случ.погр-ти пользуются понятиями теор.вер: 1)мат.ожидание
5.Оценка случайных
погрешностей измерений.основные законы распределения случ.погрешностей.при
оценке случ.погр-ти пользуются понятиями теор.вер: 1)мат.ожидание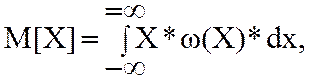 -для непрерывн.случ вел-ны, где
ω(Х)-вероятностный закон распределения сл.вел.
-для непрерывн.случ вел-ны, где
ω(Х)-вероятностный закон распределения сл.вел. 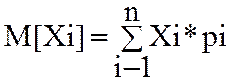 -для
дискретной сл.вел,где pi-вероятность
появления сл.вел, Хi-сл величина.
Мат.ожидание-это неслучайная вел-на,относительно ктр-ой рассеиваются другие
значения случ.вел-ны.2)закон распределения(ниже б/т). 3)дисперсия-вел-на,ктр
характеризует отклонения отн-но мат.ожидания.
-для
дискретной сл.вел,где pi-вероятность
появления сл.вел, Хi-сл величина.
Мат.ожидание-это неслучайная вел-на,относительно ктр-ой рассеиваются другие
значения случ.вел-ны.2)закон распределения(ниже б/т). 3)дисперсия-вел-на,ктр
характеризует отклонения отн-но мат.ожидания.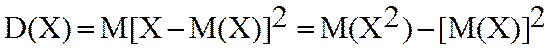 .чем
меньше D,тем точнее измерения.
4)СКо-среднеквадратичное отклонение
.чем
меньше D,тем точнее измерения.
4)СКо-среднеквадратичное отклонение ![]() ;5)вероятность
попадания в доверительный интервал.выделяют стационарные случайные процесс-они
протекают однородно во времени с постоянной амплитудой колеблются вокруг
средней функции.
;5)вероятность
попадания в доверительный интервал.выделяют стационарные случайные процесс-они
протекают однородно во времени с постоянной амплитудой колеблются вокруг
средней функции.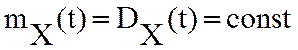 ,
, 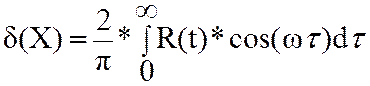 ;
;![]() -спекктральная функция хар-ет
плотность частотной реализации. случ.вел-ны м/быть описаны функциями
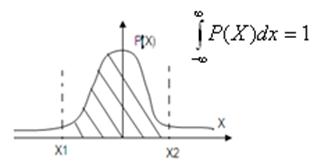
распределения.различают 1)интегральную ф-ию распределения F(x)=P{-∞<Xi≤X}
отражает вероятность события,в ктр-ом каждая случ.вел-на Xi
принимает значение < Х.
-спекктральная функция хар-ет
плотность частотной реализации. случ.вел-ны м/быть описаны функциями
распределения.различают 1)интегральную ф-ию распределения F(x)=P{-∞<Xi≤X}
отражает вероятность события,в ктр-ом каждая случ.вел-на Xi
принимает значение < Х.

 2)м/быть дифференциальной:
2)м/быть дифференциальной: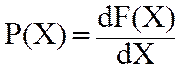 (закон распределения)
(закон распределения)

 Основные з-ны
распределения:1гр:распределении Гаусса
Основные з-ны
распределения:1гр:распределении Гаусса ![]() ,
,
![]() =2 -нормальное распределение Гаусса,
=2 -нормальное распределение Гаусса,![]() =1-распр.Лапласса. чем больше
=1-распр.Лапласса. чем больше ![]() ,тем ближе к трапецеидальному ,а при
,тем ближе к трапецеидальному ,а при ![]() =∞,распред-ие становится равномерном.
Центральная теорема теор.вер:распределение случ.погр-ти будет близкой к
нормальному всегда,когда на рез-ты измерения влияюет множество
факторов,действие каждого из ктр-ых в отдельности незначительно по сравнению с
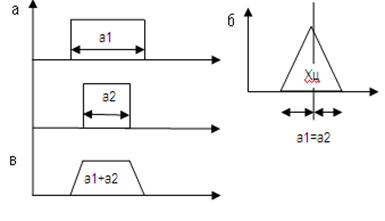
суммирующим действием всех остальных.2гр:трапецеидальное
распр-ие:равномерное(а),треугольное(б)и иснтиннотрапецеидальное(в).
=∞,распред-ие становится равномерном.
Центральная теорема теор.вер:распределение случ.погр-ти будет близкой к
нормальному всегда,когда на рез-ты измерения влияюет множество
факторов,действие каждого из ктр-ых в отдельности незначительно по сравнению с
суммирующим действием всех остальных.2гр:трапецеидальное
распр-ие:равномерное(а),треугольное(б)и иснтиннотрапецеидальное(в).
3гр:уплощенная расп-ие-композиция из экспоненциального и равномерного.
5.Оценка случайных погрешностей измерений.продолжение
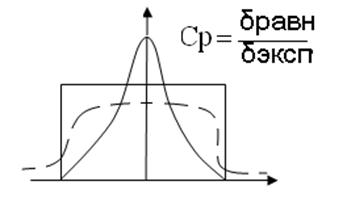
4гр:Семейство
распределения Стьюдента-они описывают плотность распределния вер-ти среднего
арифметического вероятности,вычисленного по выборке из n-случайных
отсчетов нормально распределенной генеральной совокупности.![]() ,где К-число степеней
свободы,зависящей от n.
Если K→∞,то n→∞-распределение
Гаусса. Если К→1-расп-ие Каши. 5гр: 2-хмодальное распределние: а)остро- и
кругловершинные 2-хмодальные распр-ия.
,где К-число степеней
свободы,зависящей от n.
Если K→∞,то n→∞-распределение
Гаусса. Если К→1-расп-ие Каши. 5гр: 2-хмодальное распределние: а)остро- и
кругловершинные 2-хмодальные распр-ия. ![]()
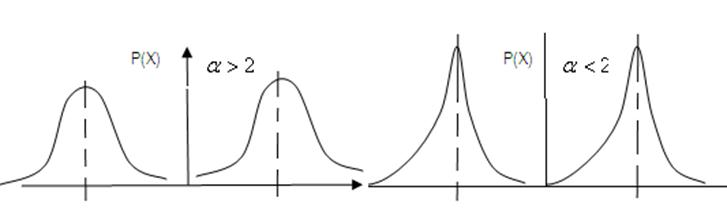
Хар-ся коэффициентом,
ктр-ый показывает процентное соотношение экспоненциального и дискретного
распределения.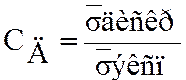
Когда СД=0-провала нет.
6.оценка грубых
погрешностей.критерий Романовского. 1)критерий 3-х сигм. 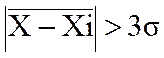 ,
, ![]() и
и
![]() рассчитываются без учета Хi.
Если
рассчитываются без учета Хi.
Если 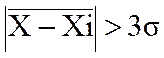 , то это промах. Вести расчет дальше,
пока условие выполняется. Как только перестало выполнятся,то Хi-не
промах и следует пересчитать
, то это промах. Вести расчет дальше,
пока условие выполняется. Как только перестало выполнятся,то Хi-не
промах и следует пересчитать ![]() и
и ![]() .
.
2)критерий Романовского : для числа измерений меньше 20.
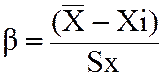 -вычисляется и сравнивается с
-вычисляется и сравнивается с ![]() . Когда
. Когда ![]()
![]() и
и ![]() рассчитываются
без учета Xi.
рассчитываются
без учета Xi.
Пример, получили след рез-ты измерения:10,15,20,25,49=Xi.
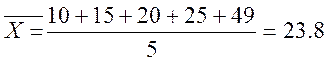
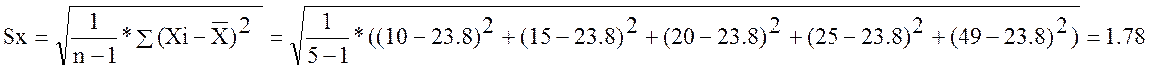
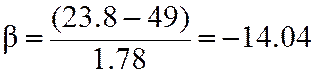 далее надо посмотреть для каких
уровней значимости значение 49 является промахом.
далее надо посмотреть для каких
уровней значимости значение 49 является промахом.
7. Порядок оценки результирующей погрешности процесса измерений
1. Оценка грубых
погрешностей результатов измерений и их устранение, например, используя
критерий Романовского: сначала определяют среднеарифметическое всех измерений ![]() , затем СКО
, затем СКО ![]() .
Находят
.
Находят 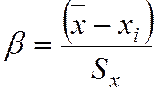 и сравнивают его с
и сравнивают его с ![]() . Если
. Если ![]() -
то
-
то ![]() промах и отбрасывается из измерений.
промах и отбрасывается из измерений.
2. 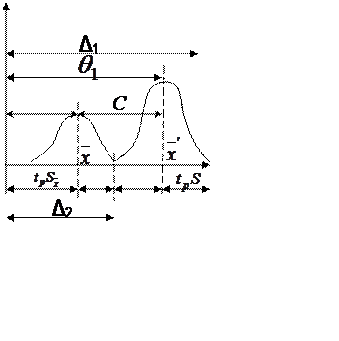 Оценка систематической погрешности и
введение поправки
Оценка систематической погрешности и
введение поправки
![]()
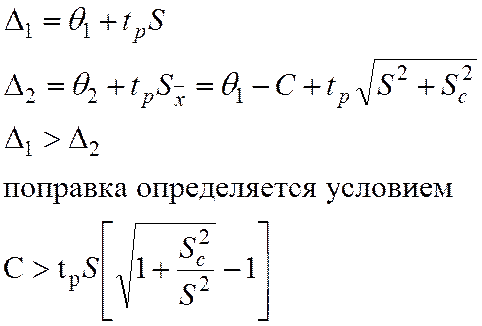
3. Оценка доверительного интервала неисключенной систематической погрешности
4. Оценка доверительного интервала случайной погрешности
5. оценка результирующей погрешности как сумма систематической и случайной.
Если справедливо неравенство ![]() , где
, где ![]() -
граница неисключенной систематической погрешности, S–СКО случайной
погрешности, то систематической можно пренебречь:
-
граница неисключенной систематической погрешности, S–СКО случайной
погрешности, то систематической можно пренебречь: 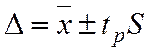 .
Если справедливо
.
Если справедливо ![]() , то
, то![]() и
можно пренебречь случайной.
и
можно пренебречь случайной.
Если 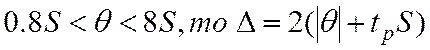
8. Структурная схема СИ прямого преобразования. Чувствительность. Преобразования.
 |
…
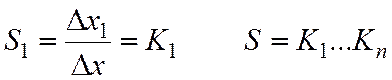
![]() определяет мультипликативную
погрешность
определяет мультипликативную
погрешность
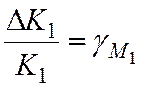 ,
,
![]() -мультипликативная погрешность
-мультипликативная погрешность ![]()
Изменение чувствительности каждого из звеньев приведет к возникновению мультипликативной погрешности, которая увеличивается с увеличением числа звеньев. Аддитивную погрешность обуславливает дрейф нуля звеньев.
 |
 …
…
Аддитивная погрешность данного типа прямого преобразования также зависит от числа звеньев. Средство измерения с такой структурой является невысокочастотным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.