Составление СДНФ и СКНФ исходной функции и их оптимизация

Дана переключательная функция:

Требуется :

1  Составить СДНФ и СКНФ исходной функции

1.1  Таблично

1.2  Аналитически

2  Оптимизировать любую из этих функций по вашему выбору

2.1  Аналитически

2.2  По карте Карно

3  Составить схемы

3.1  По оптимизированной переключательной функции на любых логических элементах

3.2  По не оптимизированной переключательной функции   на элементах

3.2.1  ИЛИ-НЕ, ИЛИ, НЕ

3.2.2  И-НЕ, И, НЕ

3.2.3  На любых логических элементах

            1 Составим СДНФ и СКНФ заданной переключательной функции

            1.1 По таблице соответствия

	а	b	c		J
1	0	0	0	0٧0٧0(0٧1)=0	0
2	0	0	1	0٧0٧0*1=0	0
3	0	1	0	0٧0٧0*1=0	0
4	0	1	1	1٧0٧0*1=1	1
5	1	0	0	0٧0٧0*0=0	0
6	1	0	1	0٧1٧0*1=1	1
7	1	1	0	0٧0٧1*0=0	0
8	1	1	1	1٧1٧1*1=1	1

По таблице получаем

J_СДНФ=m₁v m₂ v m₃то есть

J_СКНФ=(М₁) (М₂) (М₃) (М₄) (М₅)  то есть  

            1.2 Аналитически

     

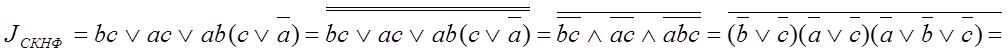
Окончательно получим

            2 Оптимизируем совершенно дизъюнктивно нормальную функцию (СДНФ)

            2.1 Аналитически

            2.2 По карте Карно

	0	0	0	0
	0	1	1	1

            Получим     

3 Схемы

3.1 По оптимизированной переключательной функции на любых логических элементах

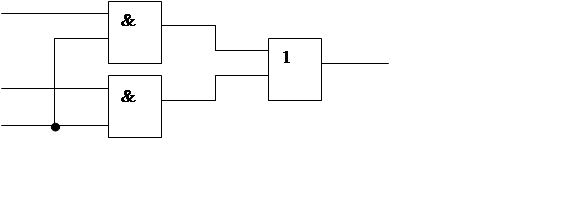                                       a            

                                                                                                          J                            

                                      b                                                                                       J

                                       c

3.2 По не оптимизированной переключательной функции   на элементах

3.2.1 ИЛИ-НЕ, ИЛИ, НЕ

Сделаем некоторые преобразования

 

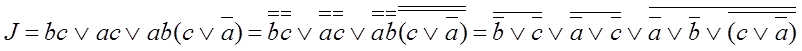
       a

                                                                                                                         J

       b

       c

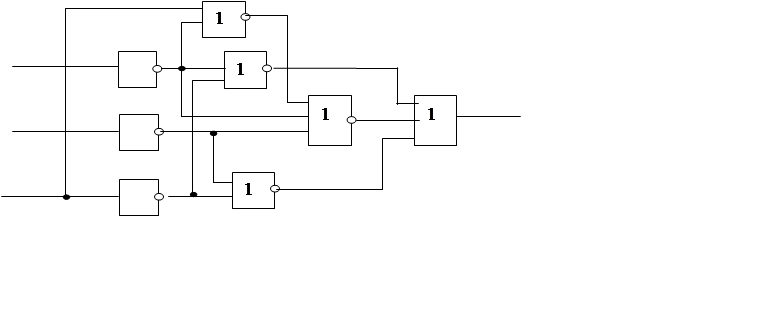
3.2.2  И-НЕ, И, НЕ

Сделаем некоторые преобразования

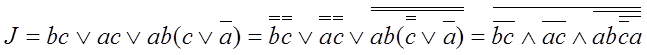
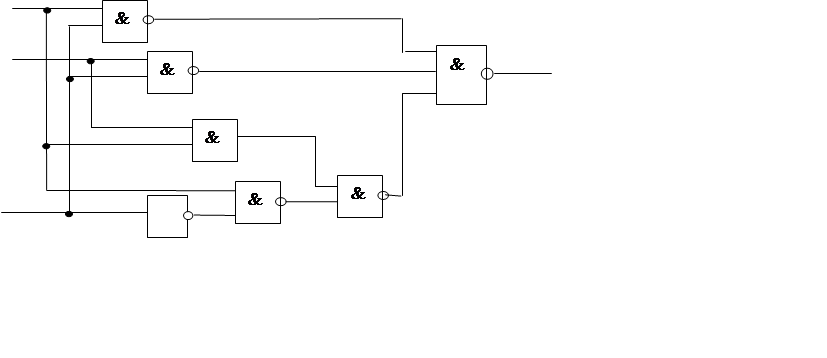     a

     b

                                                                                                                               J

                  c

3.2.4  На любых логических элементах

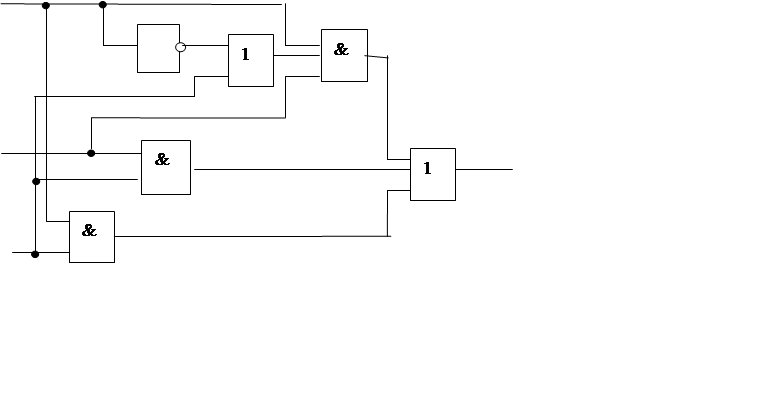                        a

                         b

                                                                                                                                       J

                         c