




Нижегородский Государственный Технический Университет
Кафедра Вычислительной техники
по дисциплине
Выполнила: студентка
группы 99-В-1
Дубровина Татьяна
Проверил: Никулин Е.А.
г.Н.Новгород 2002г.
 |
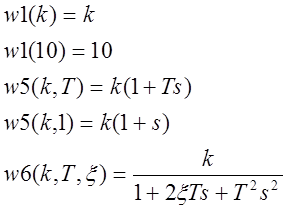
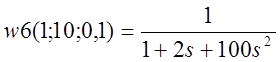
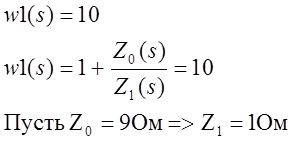 |
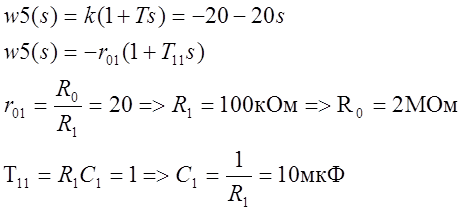 |
|||
 |
|||
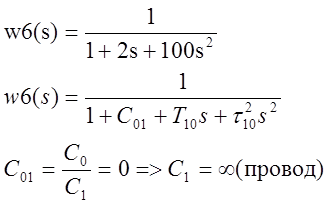 |
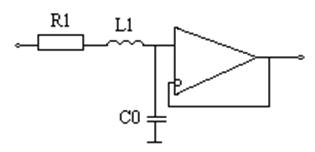
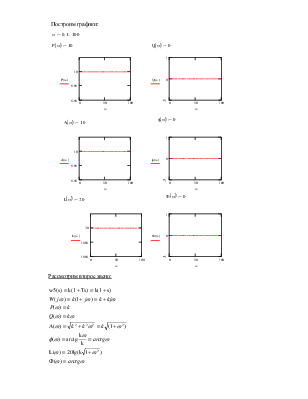
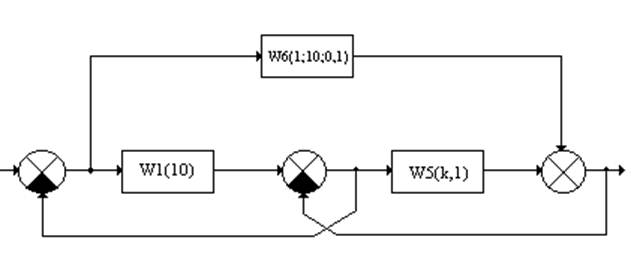
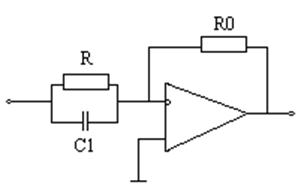
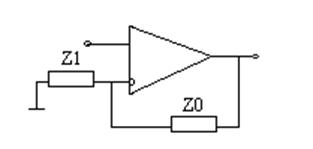
1. Получение передаточной функции для разомкнутой системы.
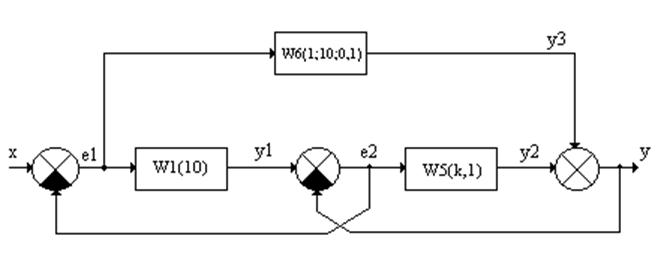
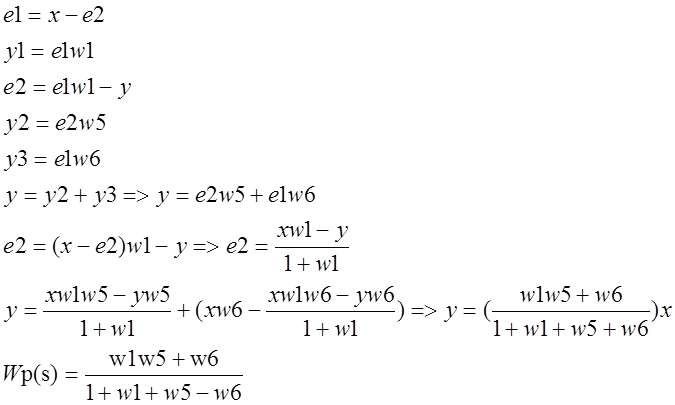
После подстановки значений ![]() получаем
передаточную функцию разомкнутой системы:
получаем
передаточную функцию разомкнутой системы:
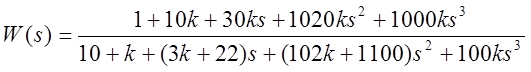
2. Построить все частотные характеристики блоков.
В соответствии с формулами
для ![]() (передаточной функции), ее мнимой и
(передаточной функции), ее мнимой и
действительной части ![]() и
и ![]() ,
построим зависимость этих величин от частоты, а также
,
построим зависимость этих величин от частоты, а также
АЧХ ![]() ,ФЧХ
,ФЧХ
![]() , ЛАЧХ
, ЛАЧХ ![]() ,
ЛФЧХ
,
ЛФЧХ ![]() и годограф
и годограф ![]() .
.
![]()
![]()
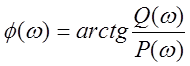
![]()
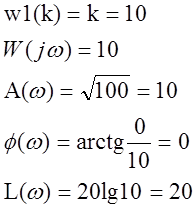 |
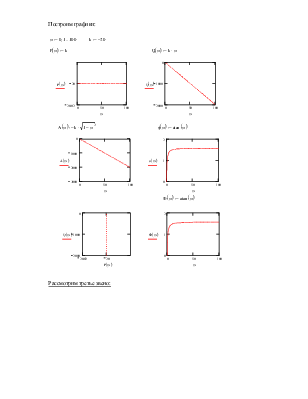
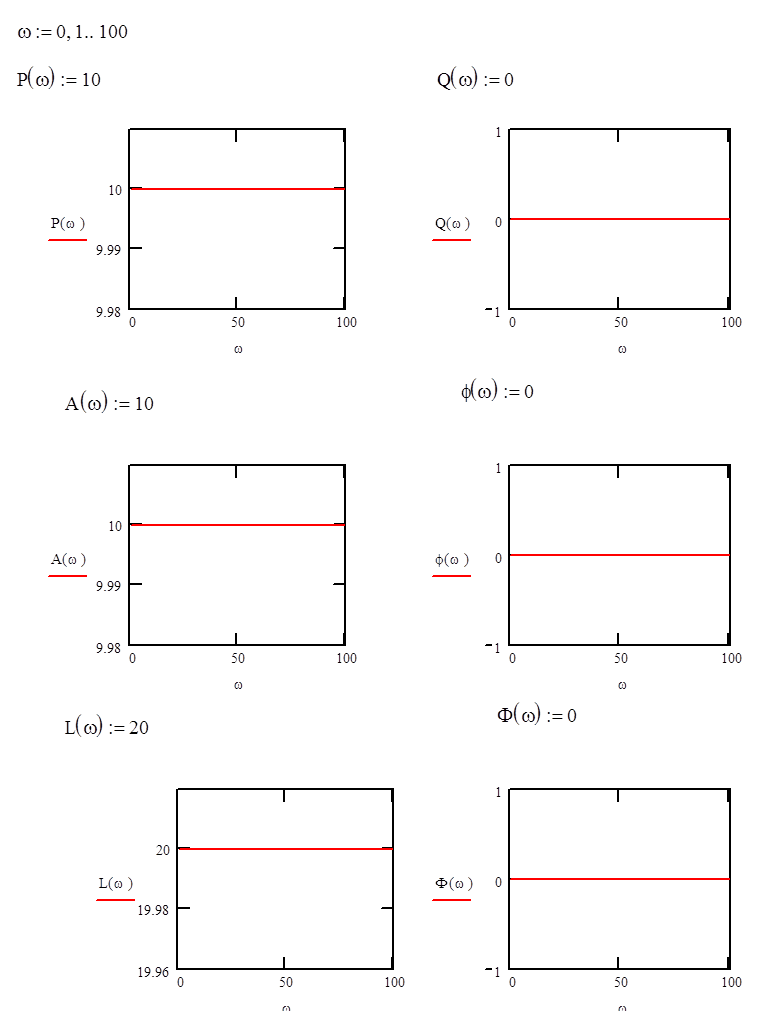
Построим графики:
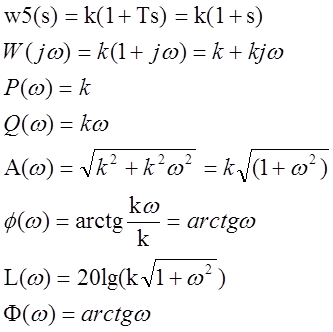 |
Построим графики:
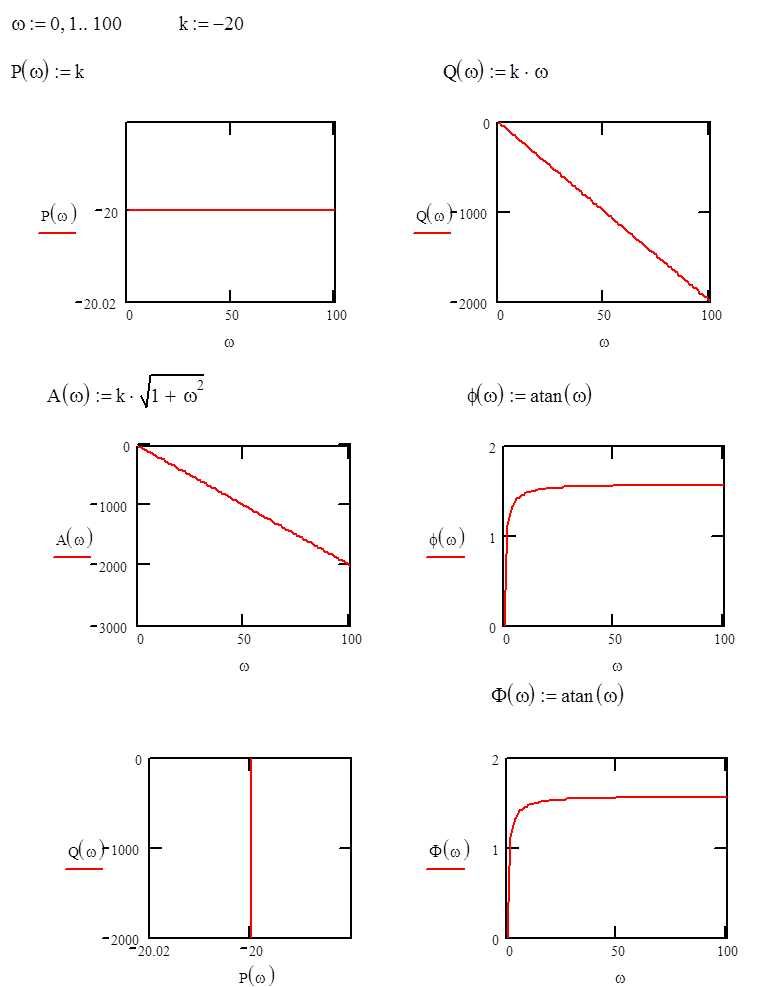
Рассмотрим третье звено:
3. Исследовать устойчивость разомкнутой системы от буквенного параметра методами
Гурвица и Михайлова.
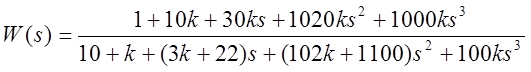
с коэффициентами ![]()
Метод Гурвица.
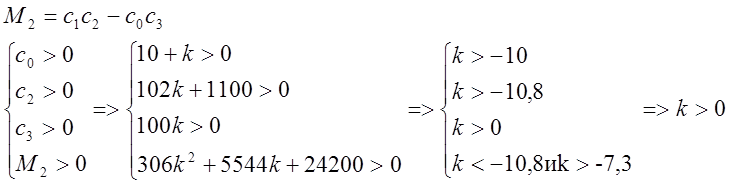
или
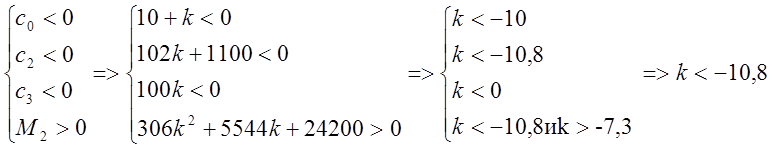
отсюда: ![]()
Метод Михайлова.
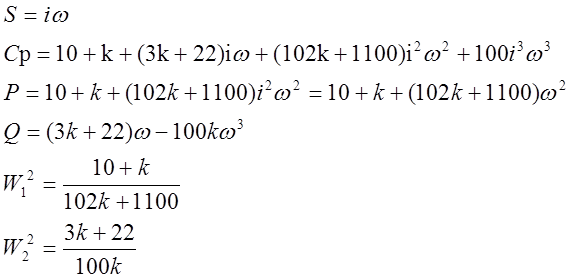
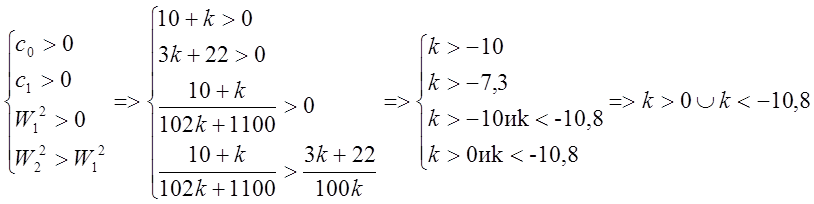
или
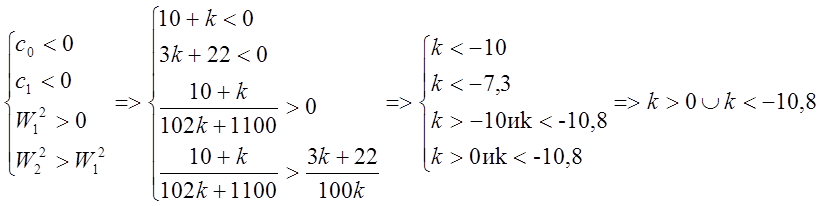
отсюда: ![]()
Исследования устойчивости по методам Гурвица и Михайлова дали одинаковые результаты.
4.Получить передаточную
функцию ![]() замкнутой единичной отрицательной
обратной
замкнутой единичной отрицательной
обратной
связью системы.
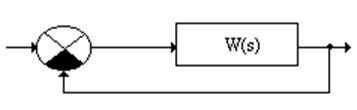
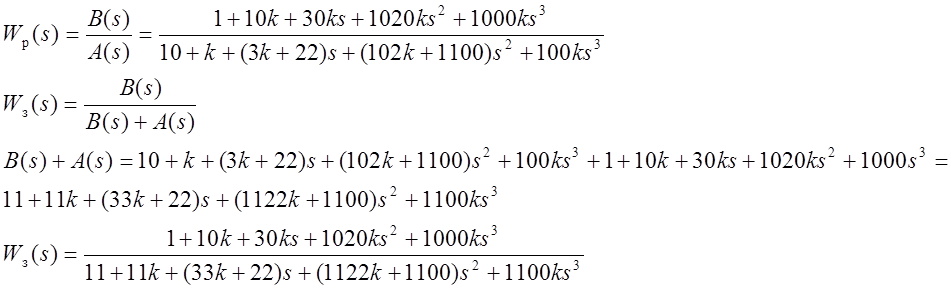
5. Исследовать устойчивость замкнутой системы от параметра методом Гурвица и Рауса
и получить диапазоны устойчивых и неустойчивых значений параметра в классе
вещественных чисел.
Метод Гурвица
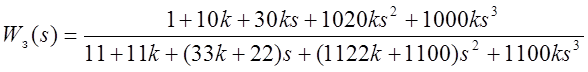
![]()
Корни полинома: ![]()
Матрица Гурвица:
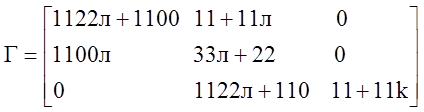
![]() должны
быть одного знака.
должны
быть одного знака.
Второй минор матрицы:
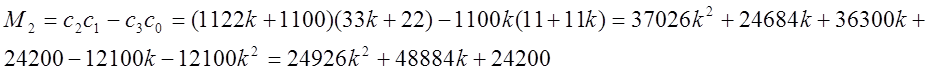
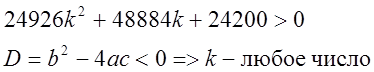
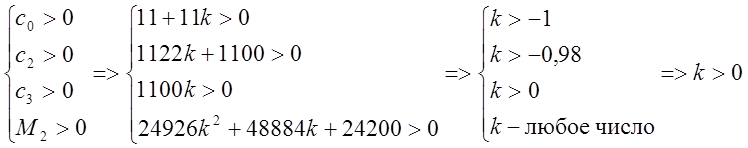
или
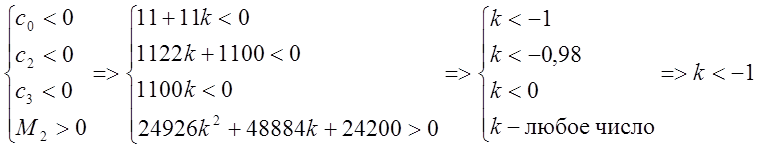
отсюда ![]()
Метод Рауса.
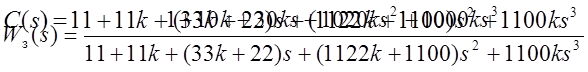 |
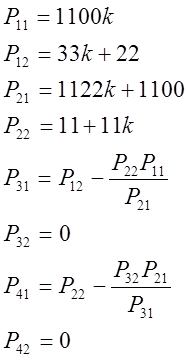
Окончательно имеем:
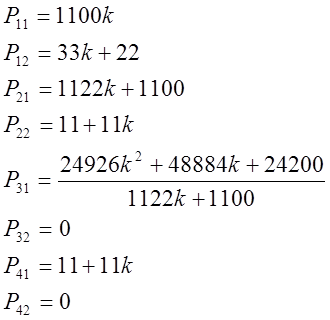
По критерию Рауса:
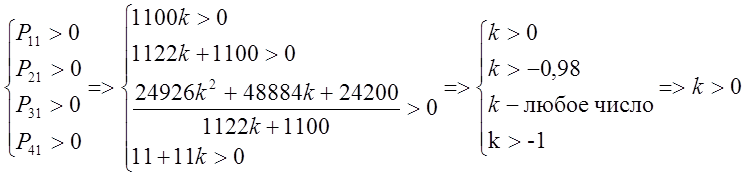
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.