Возьмем штифтовое соединение. Справочные данные:
Диаметр штифта dш=10 мм [1, т.17.2]
Длина штифта lш=60 мм [1, т.17.2]
Расстояние от края муфты до середины штифта l=25мм [1, т 17.2]
2.4 Расчет штифта на прочность
Штифт рассчитывается на прочность при срезе:
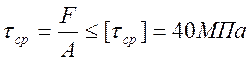 , где
, где ![]() - допускаемое напряжение среза штифта.
- допускаемое напряжение среза штифта.
Сила, действующая на штифт:
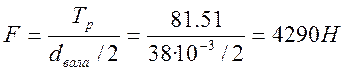
Площадь среза:
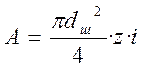 , где z=1 – количество штифтов, i=2 – количество плоскостей среза.
, где z=1 – количество штифтов, i=2 – количество плоскостей среза.
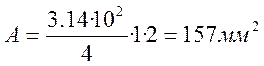
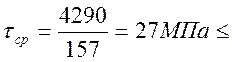
![]()
![]()
Найденное значение меньше допустимого.
3 РАСЧЕТ ЗАКРЫТОЙ ЗУБЧАТОЙ КОНИЧЕСКОЙ ПЕРЕДАЧИ
Вращающий момент на валу шестерни Т1=54,34
Н*м при частоте вращения ![]() , угловой
скорости вращения:
, угловой
скорости вращения:  , передаточное число конической передачи: U1=2,8, вращающий момент на валу колеса Т2=
, передаточное число конической передачи: U1=2,8, вращающий момент на валу колеса Т2=![]() Н*м.
Н*м.
Для изготовления шестерни выбираем сталь 40Х, улучшенную с твердостью НВ 270, для изготовления колеса – сталь 40Х улучшенную с твердостью НВ 245 [1, т. 11.6]
3.1. Расчет передачи на прочность
Определение контактного допускаемого напряжения:
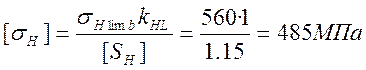 , здесь принято для колеса
значение предела контактной выносливости:
, здесь принято для колеса
значение предела контактной выносливости: ![]()
![]() - коэффициент долговечности, [SH]=1.15 – коэффициент безопасности [2,
т. 3.2]
- коэффициент долговечности, [SH]=1.15 – коэффициент безопасности [2,
т. 3.2]
КНβ=1,35-коэффициент учитывающий распределение нагрузки по зубьям при консольном расположении шестерни [2, т. 3.1]
Коэффициент ширины венца по отношению к внешнему конусному расстоянию: ψbRe=0.285 (рекомендация ГОСТ 12289-76)
Внешний делительный диаметр колеса рассчитывается по формуле:
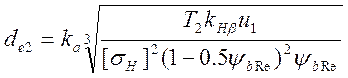 .
.
Для прямозубых передач принимается ka=99, подставим данные:
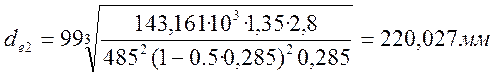
Принимаем по ГОСТ 12289-76 ближайшее стандартное значение ![]() .
.
Примем число зубьев шестерни z1=25, тогда число зубьев колеса:
z2=z1*u1=25*2.8=70
Внешний окружный модуль:
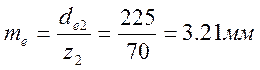
Углы делительных конусов:
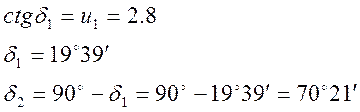
Внешнее конусное расстояние Re и длина зуба b рассчитывают по формулам:
![]()
![]() =
=![]()
Внешний делительный диаметр шестерни:
![]()
Средний делительный диаметр шестерни:
![]()
Внешний диаметр шестерни и колеса (по вершинам зубьев):
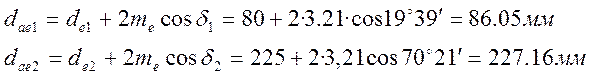
Средний окружный модуль:
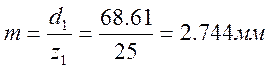
Коэффициент ширины шестерни по среднему диаметру:
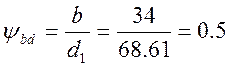
Средняя окружная скорость колес
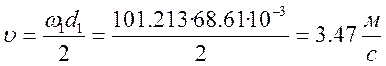
Для проверки напряжений определяем коэффициент нагрузки:
KH=KHα*KHβ*KHυ,
где KHβ=1,195 – коэффициент, учитывающий распределение нагрузки по
длине зуба при консольном расположение колес, твердости НВ<350, при ![]() =0,5 [2, т.3.5];
=0,5 [2, т.3.5];
KHα=1 – коэффициент, учитывающий распределение нагрузки между прямыми зубьями [2, т.3.4]
KHυ=1.05 – коэффициент, учитывающий динамическую нагрузку в
зацеплении для прямозубых колес при ![]() ≤5м/с
[2, т.3.6]
≤5м/с
[2, т.3.6]
Таким образом, KH=1,195*1*1,05=1,255.
Проверяем контактное напряжение:
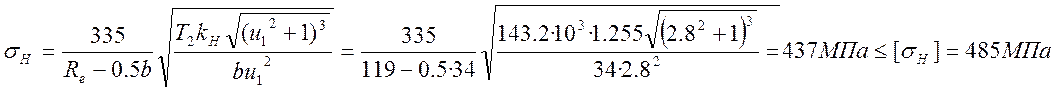 Силы в зацеплении (окружная
сила):
Силы в зацеплении (окружная
сила):
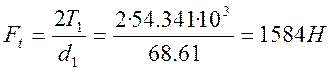
Радиальная сила для шестерни, равная осевой силе для колеса:
![]()
Радиальная сила для колеса, равная осевой силе для шестерни:
![]()
Проверка зубьев на выносливость по напряжениям изгиба:
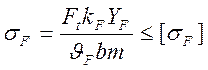 , где kF – коэффициент нагрузки, YF – коэффициент формы зуба,
, где kF – коэффициент нагрузки, YF – коэффициент формы зуба, ![]() =0.85 - коэффициент долговечности,
=0.85 - коэффициент долговечности, ![]() - допускаемое напряжение при
проверке зубьев на выносливость по напряжению изгиба.
- допускаемое напряжение при
проверке зубьев на выносливость по напряжению изгиба.
kF = KFβ*KFυ , где KFβ-коэффициент распределения нагрузки по ширине зуба; KFυ-коэффициент динамичности нагрузки.
KFβ =1,305, при ![]() =0,5, консольном
расположении колес, валах на роликовых подшипниках и твердости НВ<350 [2,
т.3.7]
=0,5, консольном
расположении колес, валах на роликовых подшипниках и твердости НВ<350 [2,
т.3.7]
KFυ =1,45, при твердости НВ<350 и скорости 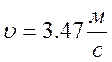 [2, т.3.8].
[2, т.3.8].
Итак, kF = 1,305·1,45=1,892.
YF – коэффициент формы зуба выбираем в зависимости от эквивалентных чисел зубьев:
для шестерни: zυ1=z1/cosδ1=25/cos ![]() ≈27,
≈27,
для колеса: zυ2=z2/cos δ2=70/cos ![]() ≈208.
≈208.
При этом YF1 =3,88, YF2 =3,6 [2, с.42]
Допускаемое напряжение при проверке зубьев на выносливость по
напряжению изгиба: 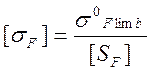 , для стали 40Х улучшенной при
твердости HB<350 предел контактной выносливости зубьев
при изгибе
, для стали 40Х улучшенной при
твердости HB<350 предел контактной выносливости зубьев
при изгибе ![]() =1.8·HB [2, т.3.9]
=1.8·HB [2, т.3.9]
Для шестерни: ![]()
Для колеса: ![]()
Коэффициент запаса прочности: ![]() ,
по [2, т.3.9]
,
по [2, т.3.9] ![]() =1,75, для поковок и штамповок
=1,75, для поковок и штамповок ![]() =1,
=1, ![]() =1,75·1=1,75.
=1,75·1=1,75.
Допускаемые напряжения изгиба при расчете зубьев на выносливость:
для шестерни: 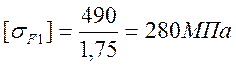
для колеса: 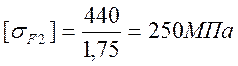
Определим наименее прочное колесо передачи по отношению [σF]/yF:
для шестерни: [σF1]/yF1=280/3,88≈72МПа
для колеса: [σF2]/yF2=250/3,6≈70МПа
Дальнейший расчет ведем для зубьев колеса, так как полученное отношение для него меньше. Проверяем зуб колеса.
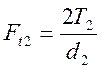 ,
где d2 - средний
делительный диаметр колеса, Ft2
– окружное усилие, действующее на зуб колеса.
,
где d2 - средний
делительный диаметр колеса, Ft2
– окружное усилие, действующее на зуб колеса.
![]()
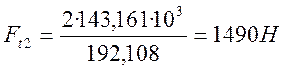
Напряжение изгиба зуба колеса:
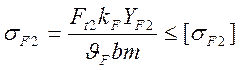
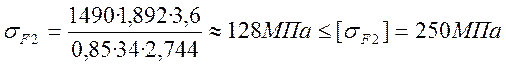
3.2. Расчет соединения колеса конической передачи с валом.
Посадочный диаметр на промежуточный вал 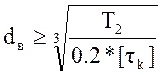 , где : :
исел зубтьт эвках и напряжением изгибастерни:для прямозубых м расположение
колес, твердости НВ, [τk]=25МПа -пониженное допускаемое напряжение при кручении;
, где : :
исел зубтьт эвках и напряжением изгибастерни:для прямозубых м расположение
колес, твердости НВ, [τk]=25МПа -пониженное допускаемое напряжение при кручении;
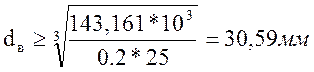 ,
примем dв=31мм, тогда длина ступицы: LCT=1,2·31≈38мм.
,
примем dв=31мм, тогда длина ступицы: LCT=1,2·31≈38мм.
Подберем прямобочное шлицевое соединение по диаметру вала из средней серии [1, т.4.5]:
z=6 – количество зубьев,
d=26мм – диаметр впадин зубьев,
D=32мм – диаметр выступов зубьев,
dср=29мм – средний диаметр шлицевого соединения,
b=6мм – ширина зуба,
l= LCT=38мм - длина шлицевого соединения.
Рассчитаем шлицевое соединение на прочность. Расчет ведем на смятие, тогда напряжение смятия:
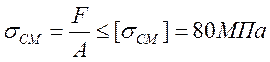 ,
,
где ![]() - допускаемое напряжение смятия,
- допускаемое напряжение смятия,
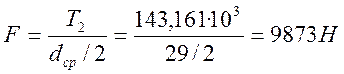 - сила, действующая на шлицы,
- сила, действующая на шлицы,
![]() - площадь смятия.
- площадь смятия.
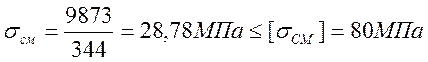 , необходимое условие на
прочность соблюдается.
, необходимое условие на
прочность соблюдается.
3.3. Конструктивные особенности конического колеса.
Подберем размеры для конической передачи [2, т.10.1]:
длина ступицы LCT =38мм,
диаметр вала dв=31мм,
диаметр ступицы dст=1.6dв=1,6·31≈50мм,
внешнее конусное расстояние Re =119мм,
ширина зуба b=34мм,
внешний диаметр выступов зубьев колеса: dae2=227мм
толщина диска колеса: С=025b=0.25·34≈9мм,
толщина зубчатого венца δ0=3,5m=3.5·2.744≈10 мм
4 РАСЧЕТ ЗАКРЫТОЙ ПРЯМОЗУБОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ
Вращающий момент на валу шестерни Т2=![]() Н*м при угловой скорости вращения:
Н*м при угловой скорости вращения: 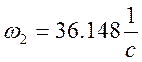 , передаточное число цилиндрической
передачи: U2=4, вращающий момент на валу колеса Т3=544,428
Н*м
, передаточное число цилиндрической
передачи: U2=4, вращающий момент на валу колеса Т3=544,428
Н*м
Для изготовления шестерни выбираем сталь 45, с твердостью НВ 230, для изготовления колеса – сталь 45 с твердостью НВ 200 [1, т. 11.6]
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.