



В начале расчета проведем идентификацию величин.
Входное возмущение f(x, t)
![]() .
.
Начальные условия:
![]()
Граничные условия:
![]() ;
;![]()
a = b = c = 1;
l =1.
Bсходные уравнения примут вид:
![]() ;
;
![]() ;
;
![]()
Выходная величина запишется в виде уравнения:
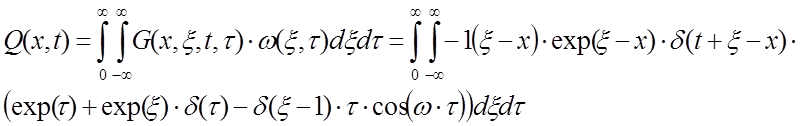
Вычислим изображение по Лапласу нормирующей функции w(x,t) и входной величины f(x,t) по формулам:
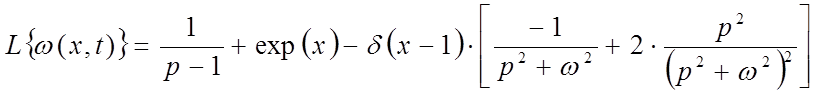 ;
;
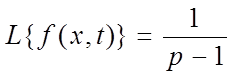 ;
;
Для определения интегральной передаточной функции необходимо найти операторное выражение выходной величины, которое будет иметь следующий вид:
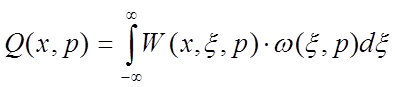
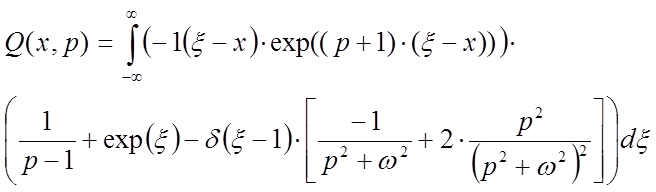
Интегральная передаточная функция определяется по формуле:
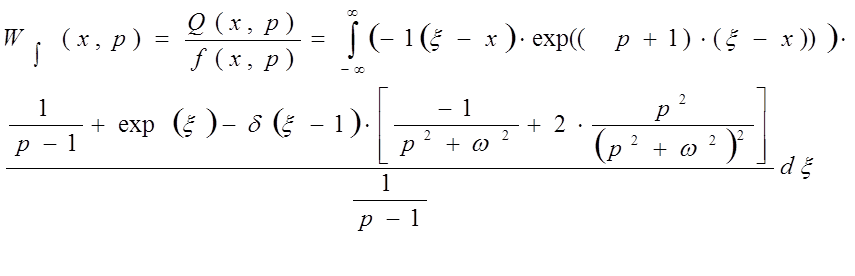
Зададим пределы интегрирования от 0 до 1 и определим значение интегральной передаточной функции в точке x=0.
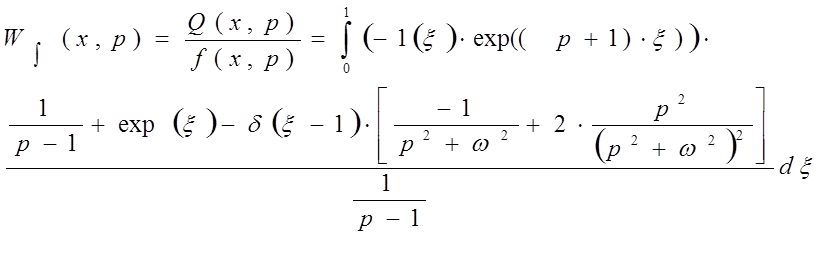
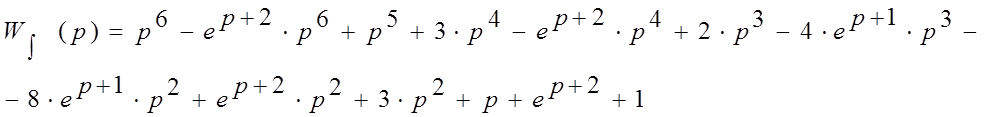
Проведем преобразования: заменим p на jw и разложим e(p) на sin и cos, выделим действительную и мнимую части.
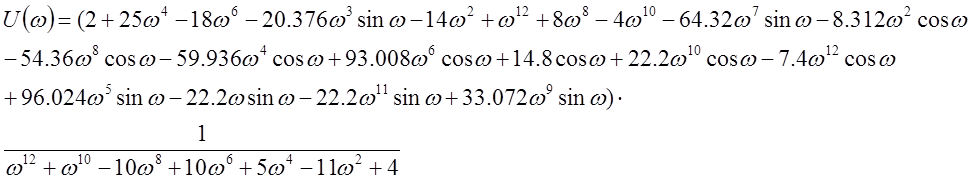
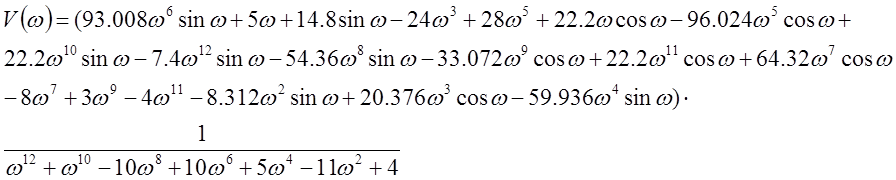
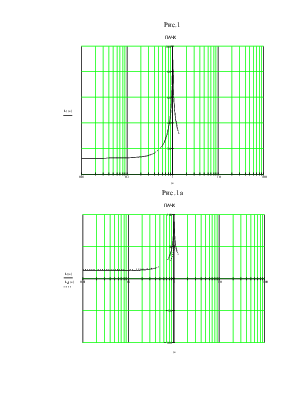
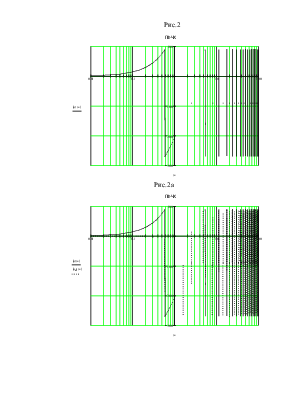
По полученным данным строим графики ЛАЧХ и ЛФЧХ (рисунки 1 и 2).
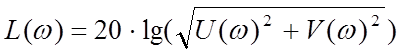 ;
;
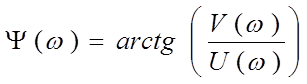 .
.
График ![]() аппроксимируем по типовыми звеньям,
см. Ю.И.Топчеев «Атлас для проектирования систем автоматического регулирования»
стр. 94-97, передаточные функции
аппроксимируем по типовыми звеньям,
см. Ю.И.Топчеев «Атлас для проектирования систем автоматического регулирования»
стр. 94-97, передаточные функции 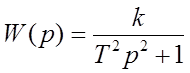 и
и 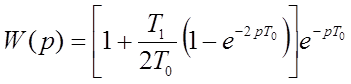 .
.
Т = 1; следует из графика L(w), т.к. именной в этой точке происходит разрыв графика.
T1 = 1;
T0 = 1.
Определим k, при w = 0
20*lgk = 14 дб/дек
k = 5.
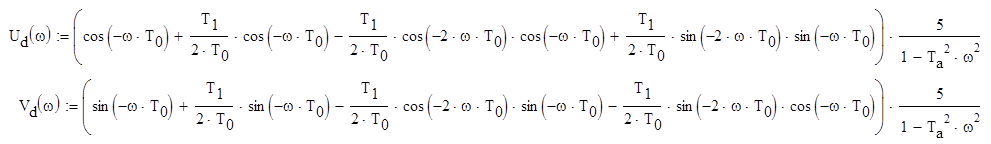
где Ta = 1.
Для интегрирующего звена ФЧХ записывается в виде:
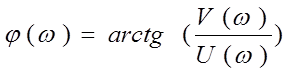 .
.
На рисунке 1 показана фактическая L(w) ЛАЧХ.
На рисунке 1а показаны фактическая L(w) и аппроксимированная Ld(w) ЛАЧХ.
На рисунке 2 изображена фактическая j(w) ЛФЧХ.
На рисунке 2a изображены фактическая j(w) и аппроксимированная jd(w) ЛФЧХ
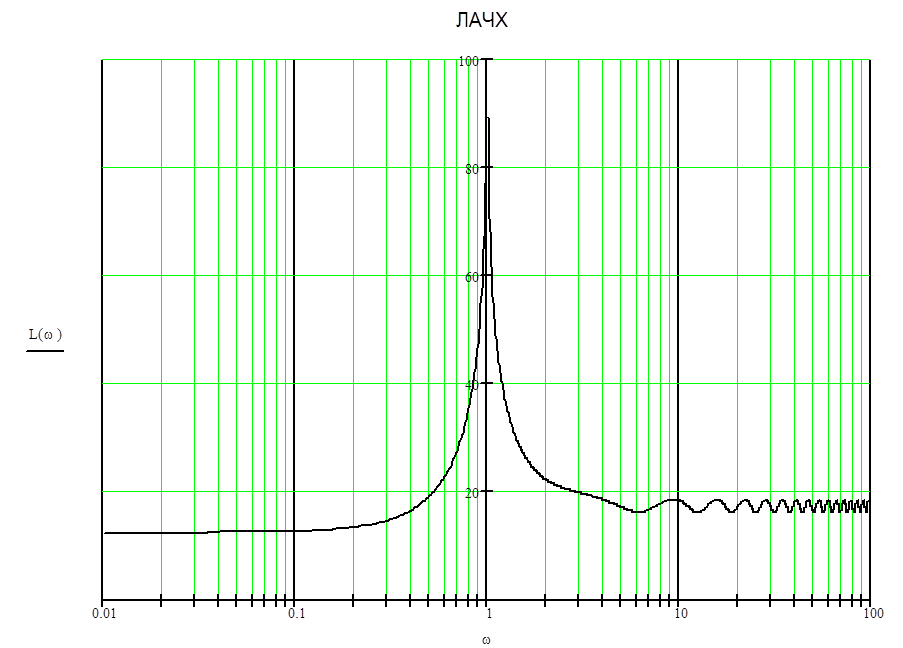
Рис.1а
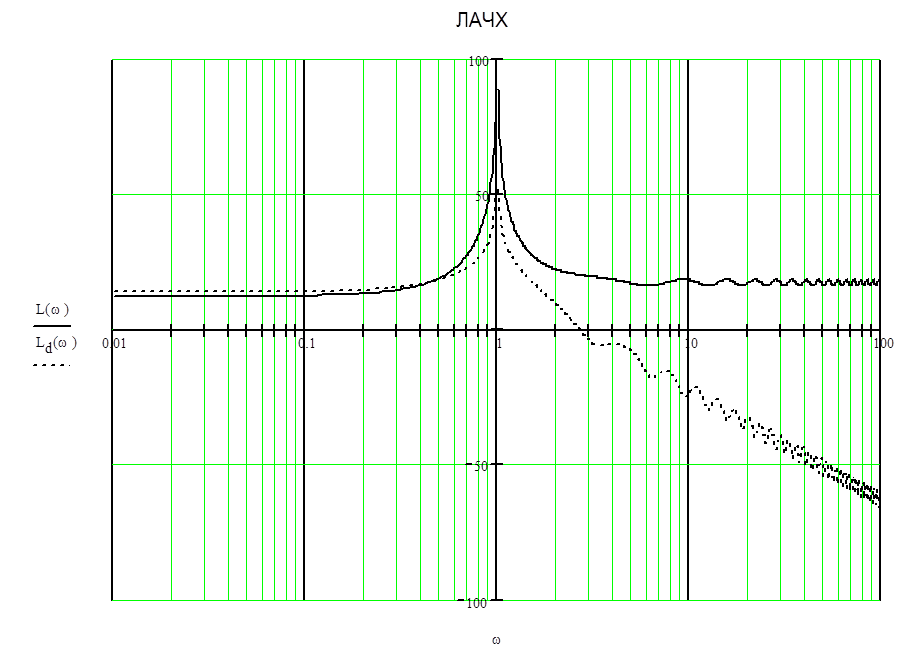
Рис.2

Рис.2а

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.