Синтез дискретного автомата. Аналіз будови, параметрів і принципу роботи інтегральних мікросхем, що реалізують логіку І-АБО-НЕ, страница 6

Після заповнення лівих п’яти стовпчиків таблиці звертаємось до ДДНФ логічного виразу.

3.6. Сума всіх ваг робочих станів дискретного автомата дорівнює 1+4+6+9+13= 33.

Синтез функціональної схеми дискретного автомата завершений, сума ваги робочих станів дискретного автомата рівна 33.

·  Побудова принципової схеми дискретного автомата.

Задано логічний вираз

Розв’язок.  

4.1. Виражаємо задане логічне рівняння через функції І-НЕ, оскільки елементи мікросхем типу ЛА реалізують логічні функції І-НЕ:

1 спосіб :

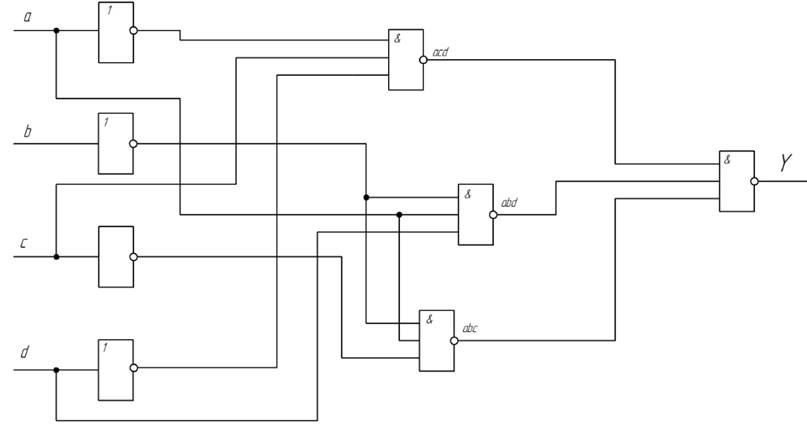
Рисунок 3.- Функціональна схема дискретного автомата в базисі НЕ,І,АБО

2 спосіб:

Якщо попередньо застосовувати до логічної суми (dvc) перетворення де Моргана, то отримаємо:

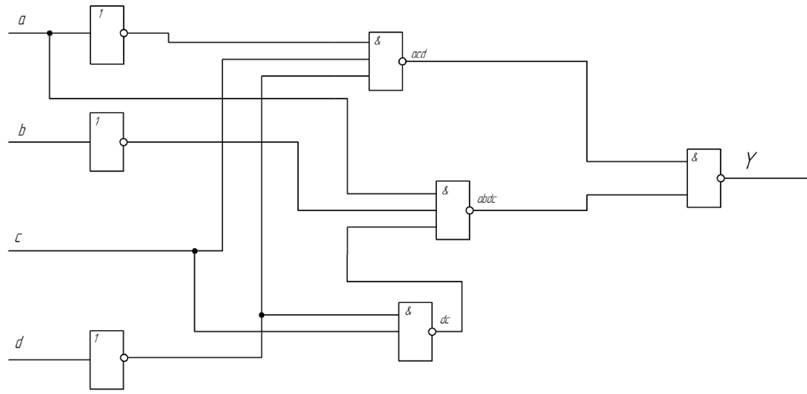
Рисунок 4.- Функціональна схема дискретного автомата в базисі І-НЕ

Проаналізувавши перший і другий варіант логічного виразу ми з’ясували, що у першому випадку (рис. 3) нам потрібно чотири три входових елементів 3І-НЕ, і три двох входових елементів 2І-НЕ, які використовуються в якості інверторів вхідних сигналів. В свою чергу для реалізації другої схеми нам потрібно п’ять двох входових елементів 2І-НЕ, і два три входових елементів 3І-НЕ. Звідси ми бачимо, що другий варіант більш підходящий. Оскільки для нього потрібно одну мікросхему ЛА3 і одну мікросхему ЛА4.

Отже, синтез дискретного автомата проводимо за останнім логічним виразом.

4.2. Отримаємо функціональну схему дискретного автомата (рис. 4).

4.3. Для побудови принципової схеми вибираємо одну мікросхему К155ЛА3 і одну К155ЛА4.  Мікросхеми ЛА3 містить чотири двох входові елементи 2І-НЕ, у випадку об’єднання  входів, дозволяють отримати інвертори для сигналів a, b, c, d. Мікросхема ЛА4 містить три тривходових елементи 3І-НЕ.

4.4. Заміняємо елементи функціональної схеми позначеннями вибраних елементів ( рис. 5).

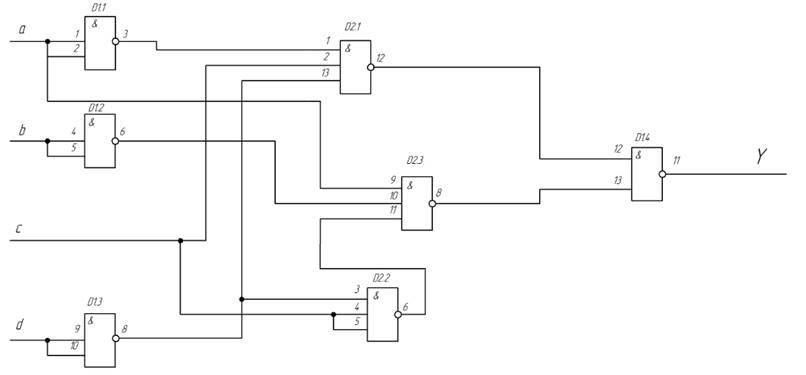
Рисунок 5. - Принципова схема дискретного автомата без пам’яті

4.5. Розмічаємо входи елементів задіяних мікросхем. Нумерація вводів мікросхем, що використовується, наведена на рис. 6. Проставляємо позиційне позначення елементів. Отримаємо принципову схему дискретного автомата.

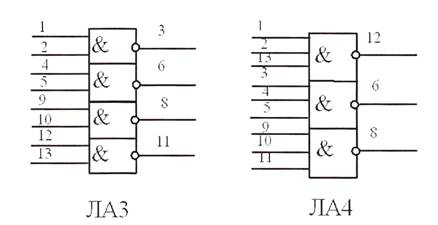
Рисунок 6. - Умовні позначення мікросхем класу ЛА

4.6. Проводимо аналіз умов функціонування дискретного автомата, виконуючи пункти в, г, д, е методики синтезу функціональної схеми. Рівність суми ваги робочих станів принципової схеми дискретного автомата та його функціональної схеми підтверджують правильність логічного синтезу ДА.

4.7. Технічна реалізація синтезованої схеми дискретного автомата можлива, оскільки:

- в синтезованій схемі коефіцієнт об’єднання входів елементів не більше 2. В логічних елементах мікросхем типу ЛА можливе  об’єднання 8-10 входів;

- коефіцієнт розгалуження задіяних елементів рівний 3, що значно менше нормативного значення К_р=10.

Висновок: синтезована схема дискретного автомата працездатна.

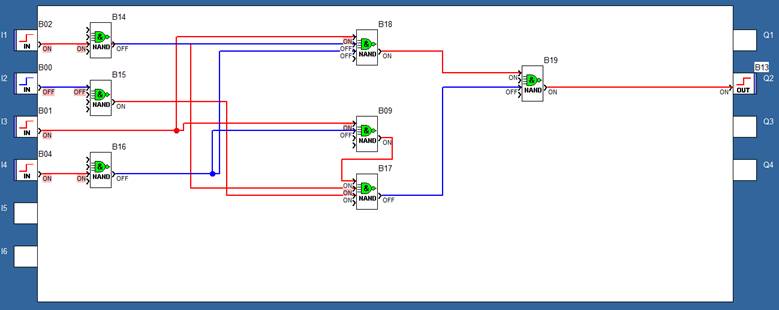
4.8. Проводимо перевірку роботи  дискретного автомата в середовищі Zelio Soft2, використовуючи ДДНФ виразу і таблицю 3.

Реалізація принципової схеми ДА в середовищі Zelio Soft2 для логічної умови :

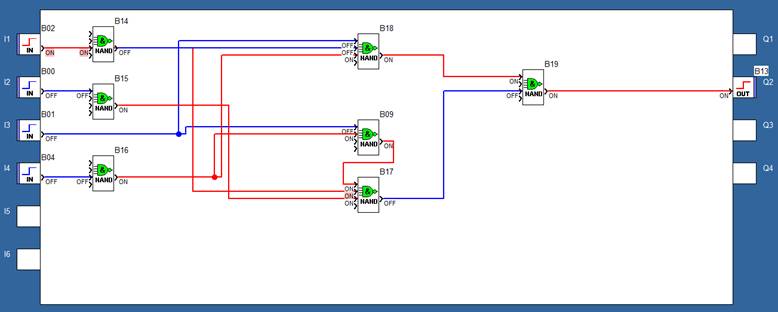
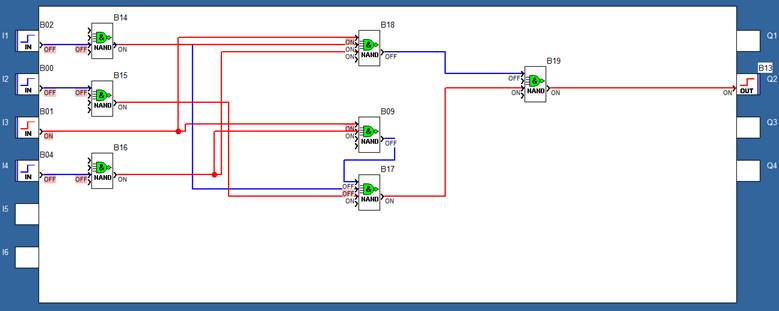
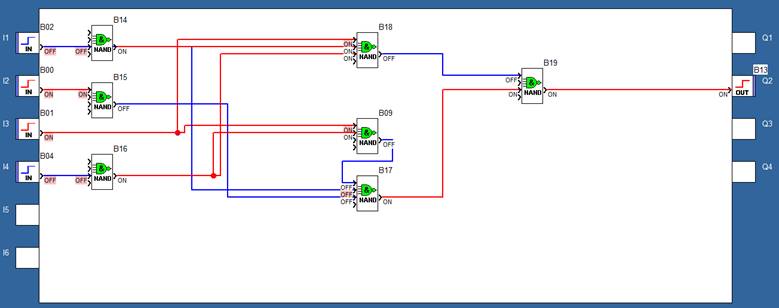
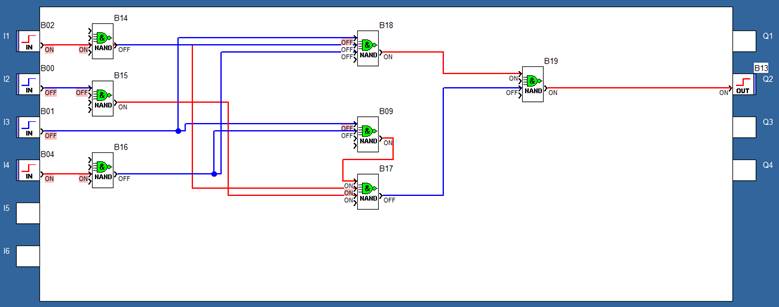
ЗАВДАННЯ №4

·  Синтез принципової схеми дискретного автомата з пам’яттю

Формула включення виконавчого елемента має вигляд:

Умови функціонування дискретного автомата визначаються логічними виразами:

Використовуються формувачі вхідних сигналів F(+A), F(+B), F(+C).

Перетворювачем вихідної величини є перетворювач типу РТ. Логічними елементами є мікросхеми серії К155 типу ЛА.

Розв’язок :

·   Виразимо логічні рівняння ДА через логічні функції  І-НЕ:

5.2. Зображуємо функціональну схему власне дискретного автомата за допомогою функціональних логічних елементів І-НЕ (рис. 7).

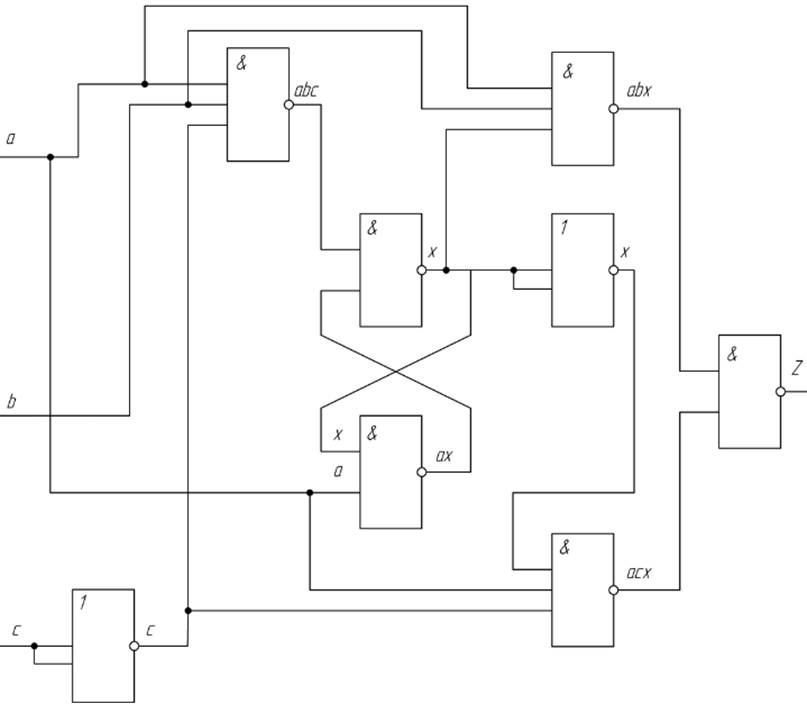
Рисунок 7. - Функціональна схема дискретного автомата

5.3.  Доповнюємо отриману функціональну схему зображенням формувачів і перетворювача. Формувачі F(+A), F(+B), F(+C) в початковому положенні мають на виході сигнали, що описуються прямими значеннями змінних a,b,c , які співпадають із значеннями відповідних змінних функціональної схеми