Синтез дискретного автомата. Аналіз будови, параметрів і принципу роботи інтегральних мікросхем, що реалізують логіку І-АБО-НЕ, страница 5

δ — функція переходів, яка задає відображення множин X·Z→Z;

λ — функція виходів, яка задає відображення множин X·Z→Y або Z→Y;

z₁ — початковий стан автомата.

Множини X, Y, Z називаються алфавітами, а їхні елементи — буквами. Послідовності вхідних та вихідних букв створюють відповідно вхідні та вихідні слова.

Поняття "пам'ять" (внутрішні стійкі стани) автомата введено для описування систем, сигнали на виходах яких залежать як від вхідних сигналів в даний момент часу, так і від попередньої історії розвитку процесу. Взагалі множина стійких станів автомата — це сукупність поточних значень фізичних параметрів елементів пам'яті (наприклад, напруга на виходах тригерів), яка зберігається до надходження відповідного вхідного сигналу. Внутрішній стан автомата відповідає деякій пам'яті про минуле і дозволяє усувати час як явну змінну і виражати вихідні сигнали як функцію входів і пам'яті.

Автомат працює в дискретному часі й перехід із стану в стан здійснюється миттєво. За способом введення дискретного часу автомати поділяються на синхронні та асинхронні. У синхронних автоматах дискретний час задають генератором синхросигналів: t = 0,1,2,..., де t — номер машинного такту. В асинхронних автоматах моменти переходу із одного стану в інший попередньо не визначені й залежать від деяких подій. В таких автоматах інтервал дискретності змінний.

У теорії найповніше описані й на практиці широко застосовуються синхронні автомати.

2.2. Загальні принципи синтезу дискретних систем керування

У випадку розробки схем дискретного керування, загальна методика їх складання передбачає наступний порядок:

·  формулюється задача, конкретизуються умови роботи схеми керування;

·  за допомогою логічних функцій НЕ, І, АБО здійснюється математичний опис умов роботи схеми;

·  для складних логічних систем на першій стадії етапу математичного опису складається таблиця станів системи, що проектується та проводиться перевірка складеної схеми керування;

·  складаються функціональні схеми, що реалізують окремі логічні рівняння. Створення функціональних схем супроводжується застосуванням елементарних методів мінімізації за допомогою використання сигналів, отриманих в одній частковій функціональній схемі, яка є реалізацією одного рівняння в інших аналогічних схемах.

·  після побудови схеми проводиться перевірка правильності її роботи за допомогою таблиці станів і дається оцінка кількості задіяних в схемі елементів;

·  перетворення функціональної схеми керування в принципову.

ЗАВДАННЯ № 3

·  Синтез дискретного автомата без пам’яті

3.1. Дискретний автомат має чотири входи ( прямі значення a,b,c,d ) і один вихід у.

3.2. Складаємо функціональну схему дискретного автомата ( рис. 3).

3.3. Записуємо логічний вираз вихідної величини дискретного автомата

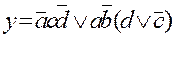
3.4. Записуємо отриманий логічний вираз в ДДНФ :

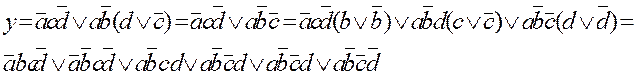
3.5. Складаємо таблицю станів дискретного автомата (таблиця 3). Таблиця має 6 стовпчиків і 16 рядків. Присвоюємо вхідним сигналам вагу:

a–2⁰, b–2¹, c–2²,d–2³.

Таблиця 3.  Стани дискретного автомата

	Вхідні сигнали та їх вага
Вага стану	a	b	c	d	y
	20	21	22	23
0	-	-	-	-	0
1	+	-	-	-	1
2	-	+	-	-	0
3	+	+	-	-	0
4	-	-	+	-	1
5	+	-	+	-	0
6	-	+	+	-	1
7	+	+	+	-	0
8	-	-	-	+	0
9	+	-	-	+	1
10	-	+	-	+	0
11	+	+	-	+	0
12	-	-	+	+	0
13	+	-	+	+	1
14	-	+	+	+	0
15	+	+	+	+	0