Повышение предела прочности при 300°С листов из титанового сплава

маркировка для более удобного восприятия дана как согласно ГОСТ 4784-97, так и согласно международному стандарту ISO 209-1.

1. Сплавы, упрочняемые давлением:

а) сплавы, обладающие низкой прочностью и высокой пластичностью. Свариваемые и коррозионно-стойкие.

К ним относятся нелегированный технический алюминий (маркировка АД0/1050А, АД1/1230 и пр.), а также алюминиевые сплавы с марганцем (АМц/3003, Д12/3004, ММ/3005);

б) сплавы, обладающие средней прочностью и высокой пластичностью. Свариваемые и коррозионно-стойкие.

К ним относятся так называемые магналии – сплавы, легированные магнием: Амг2/5251, АМг3/5754, АМг5/5056, АМг6 и пр.

2. Сплавы, упрочняемые термообработкой:

а) сплавы, обладающие средней прочностью и высокой пластичностью. Свариваемые.

К ним относятся так называемые авиали – сплавы, легированные магнием и кремнием, например АД31/6063, АД33/6061, АД35/6082;

б) сплавы, обладающие нормальной прочностью.

К ним относятся так называемые дюрали – сплавы, легированные медью и магнием, например алюминиевый сплав Д16/2024, Д1/2017, Д18/2117, а также алюминиевый сплав Д16Т и др.;

в) сплавы, обладающие нормальной прочностью. Свариваемые.

К ним относятся сплавы, легированные цинком и магнием: 1915/7005, 1925;

г) сплавы, обладающие высокой прочностью.

К ним относятся сплавы, легированные медью, магнием, никелем и железом – В95 и В93;

д) сплавы, обладающие высокой жаропрочностью.

К ним относятся сплавы, легированные медью, магнием, никелем и железом (АК4-1, АК) и сплавы, легированные медью и марганцем (1201/2219, Д20);

е) ковочные сплавы.

К ним относятся сплавы, легированные медью, магнием и кремнием (АК6, АК8/2014).

В зависимости от вида термической обработки алюминиевые сплавы маркируются следующим образом:

отожженный сплав – М;

сплав, нагартованный на ¼ – Н4;

сплав, нагартованный на ½ – Н2;

сплав, нагартованный на ¾ – Н3;

нагартованный сплав – Н.

1. ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА

План эксперимента представляет собой полуреплику от полного факторного эксперимента типа . Ее определяющий контраст 1=, следовательно, для первых трех факторов  в матрице планирования записываем полный факторный эксперимент , а столбец приравниваем к произведению столбцов , то есть . Три последних опыта в матрице планирования представляют собой опыты на основном уровне. В последнем столбце записывают результаты опытов.

Таблица 1 – Условия эксперимента

Факторы	Zn, %	Толщина листа, мм	Температуры состояния С	Время старения, час
Основной уровень()	6	9	460	14
Интервалы варьирования()	1	1	10	4
Верхний уровень (+1)	7	10	470	18
Нижний уровень (-1)	5	8	450	10

План эксперимента в таблице 2 записан в кодовом масштабе.

Запишем его в таблицу 3 в натуральном масштабе. Кроме того, с помощью случайных чисел установим порядок реализации опытов.

Таблица 2- План эксперимента в кодовом масштабе

Номер опыта						y
1	+	+	+	+	+	6,75
2	+	-	+	+	+	5,25
3	+	+	-	+	-	5,75
4	+	-	-	+	-	4,25
5	+	+	+	-	-	7,50
6	+	-	+	-	-	8,50
7	+	+	-	-	+	7,00
8	+	-	-	-	+	5,50
9	0	0	0	0	0	5,75
10	0	0	0	0	0	6,25
11	0	0	0	0	0	7,00

Таблица 3- План эксперимента в натуральном масштабе

Номер опыта	Порядок реализации опытов	Zn, %	Толщина листа, мм	Температуры состояния,°C	Время старения, час	,кг/см
1	5	7	10	470	18	6,75
2	8	5	10	470	18	5,25
3	3	7	8	470	10	5,75
4	4	5	8	470	10	4,25
5	1	7	10	450	10	7,50
6	7	5	10	450	10	8,50
7	6	7	8	450	18	7,00
8	2	5	8	450	18	5,50
9	9	6	9	460	14	5,75
10	10	6	9	460	14	6,25
11	11	6	9	460	14	7,00

Запишем систему оценок коэффициента регрессии 1=.

                                           

                                             

                                             

                                             

                                             

                                          

                                          

Таким образом, выбранное планирование позволяет построить только линейную модель:

, коэффициенты которой смешаны с эффектами тройных взаимодействий факторов; все парные эффекты смешаны между собой.

2. ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА И ПОСТРОЕНИЕ МОДЕЛИ

2.1.Определение погрешности эксперимента

Расчет дисперсии и среднеквадратичной ошибки опыта.

О способах расчета дисперсии и среднеквадратичной ошибки  опыта.

Значение  рассчитываем по результатам трех опытов (опыты 9-11 в таблице 2 и 3) на основном уровне (таблица 4).

Таблица 4

Номер
1 2 3	5,75 6,25 7,00	0,55 0,05 0,7	0,3025 0,0025 0,49

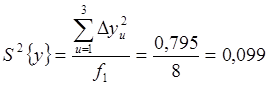
Итак, дисперсия опыта оказалась равной 0,099 при числе степеней свободы =2.

Соответственно среднеквадратичная ошибка опыта:

2.2.Расчет коэффициентов регрессии

О способах расчета коэффициентов регрессии и их доверительных интервалов.

Коэффициенты регрессии считаем по формуле:

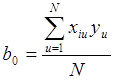
Доверительные интервалы коэффициентов рассчитываем по формуле:

Примем при этом N=8; из приложения 2:

=0,099 /8=0,012, следовательно:

Таким образом:

Сравним величины коэффициентов регрессии (по абсолютной величине) с их доверительными интервалами:

6,31 > 0,7

0,44  0,7

0,7   0,7

0,81  0,7

0,19  0,7

Таким образом, коэффициенты можно признать статистически значимым, а коэффициенты - статистически не значимыми и из модели исключаются.

Запишем линейную модель зависимости предела прочности алюминиевого сплава при 460 °С от факторов, влияющих на него:

У=6,31+0,7                      (2)

В уравнении (2) факторы входят в кодированном масштабе. От кодированных значений к натуральным и обратно можно переходить по формулам:

2.3.Проверка адекватности модели

Проверим адекватность модели (2)  по t-критерию, расчетное значение