зависимости от соотношений значений рассматриваемого и базового уровней значение коэффициента роста Нt может оказаться меньше единицы (уt < убаз), равным единице (при уt = убаз) или больше единицы (при уt > убаз).
Коэффициент роста, выраженный в процентах, называется темпом роста.
Коэффициент прироста Bt определяется как отношение абсолютного прироста At к уровню, принятому за базу для сравнения убаз:
Bt = At / убаз. (3)
Значения Bt могут быть положительными, отрицательными, либо равными нулю в зависимости от значений абсолютного прироста.
Коэффициент прироста, выраженный в процентах, называется темпом прироста. Он показывает, на сколько процентов увеличилось или уменьшилось значение рассматриваемого уровня ряда уt по сравнению с базовым убаз, принятым за 100%.
Рассмотрим таблицу 8, в которой представлены результаты расчета рассмотренных показателей для интервального временного ряда, отражающего динамику числа пожаров в городе за пять лет (N=5). За базу для сравнения с тем или иным уровнем ряда уt принят предшествующий уровень ряда (убаз = уt-1). Вычисляемые при таком условии показатели At, Нt и Bt (t = 1, 2,…, N) называются цепными.
Таблица 8
Показатели ряда динамики числа пожаров в городе за 5 лет
|
Показатели |
Годы, t |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
уt |
252 |
246 |
288 |
300 |
326 |
|
At |
– |
-6 |
42 |
12 |
26 |
|
Нt |
– |
0,976 |
1,171 |
1,041 |
1,086 |
|
Темп роста, % |
– |
97,6 |
117,1 |
104,1 |
108,6 |
|
Bt |
– |
-0,024 |
0,170 |
0,041 |
0,086 |
|
Темп прироста, % |
– |
-2,4 |
17 |
4,1 |
8,6 |
3. Эффективным способом выявления основной тенденции процесса изменения уровней временного ряда является его математическое моделирование.
Если характер динамики подтверждает предположение о том, что наблюдаемое в t-м году число пожаров в городе (районе) уt (t= 1, 2, …, N, где N – число анализируемых лет) изменяется с течением времени с более или менее постоянной абсолютной скоростью, то математическим выражением такой тенденции будет являться линейная зависимость вида:
ŷt = a+bt, (5)
где ŷ – расчетное значение числа пожаров в t-м году; a и b – коэффициенты, t – номер года.
Для нахождения неизвестных коэффициентов используется метод наименьших квадратов. Для нахождения коэффициентов а и b используются уравнения:
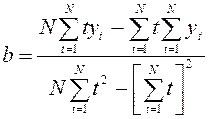 (6)
(6)
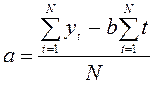 (7)
(7)
4. Зная величины коэффициентов a и b и предполагая, что имеющаяся тенденция изменения числа пожаров в городе (районе) останется неизменной, можно вычислить прогнозную оценку числа пожаров в интересующем году, поставив в уравнение (5) номер этого года.
В качестве примера выполним прогнозирование числа пожаров в городе на год вперед по заданным исходным данным числа пожаров за последние 5 лет.
Для выявления тенденции изменения числа пожаров в городе используем аналитическое выравнивание временного ряда в виде зависимости (5). Для нахождения коэффициентов a и b воспользуемся формулами 6 и 7, предварительно составив вспомогательную таблицу 9:
Таблица 9
Вспомогательная таблица для вычисления коэффициентов a и b
|
t |
t2 |
уt |
t уt |
|
1 |
1 |
252 |
252 |
|
2 |
4 |
246 |
492 |
|
3 |
9 |
288 |
864 |
|
4 |
16 |
300 |
1200 |
|
5 |
25 |
326 |
1630 |
|
15 |
55 |
1412 |
4438 |
Подставляя числовые значения из итоговой строки табл. 2 в уравнения (6 и 7) находим значения коэффициентов:
![]()
![]()
Используя уравнение (5), определяем ориентировочное значение числа пожаров в городе в следующем году (t=6):
y6 = 221,8+ 20,2∙6 = 343
Наносим на график эмпирические значения числа пожаров за прошедшие 5 лет и прогнозируемое значение для шестого года. По результатам расчета делаем вывод.
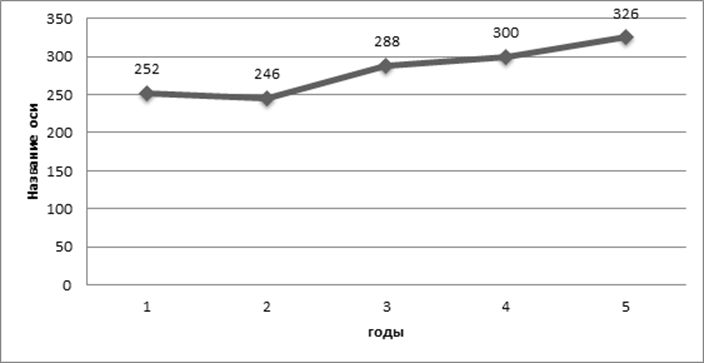
Рис. 1. Динамика числа пожаров в городе по годам.
Для рассматриваемого примера можно сделать вывод, что, несмотря на ежегодные колебания цепных показателей изменчивости временного ряда, наблюдается тенденция роста числа пожаров в городе.
1. Находим число mu пожаров в городе, которые возникли по u-той причине (u=1, 2,…, U, где U – общее число причин пожаров, которое согласно кодификатору, равно 9). Для полученных значений mu (u=1, 2,…, U), называемых абсолютными частотами, должно выполняться соотношение:
![]() mu = m, (8)
mu = m, (8)
где m – общее число пожаров за год, u – общее число причин пожаров, которое согласно кодификатору равно 9.
2. Производим вычисление доли ωu, которую в общем числе пожаров составляют пожары, возникшие по u-ой причине (u = 1, 2,…, U):
![]() u
= 1, 2,…, U. (9)
u
= 1, 2,…, U. (9)
При этом сумма всех ω u (ω1 + ω2 +… ω9), называемых относительными частотами или частностями, должно выполняться соотношение:
![]() (10)
(10)
3. Перечень различных причин пожара в абсолютном и относительном
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.