Московский Государственный Институт Электроники и Математики
Кафедра “Физические основы электронной техники”
Курсовая работа
Вариант задания №21
Выполнил:
Проверила:
Москва, 2010
Дано: ![]() ;
;
![]()
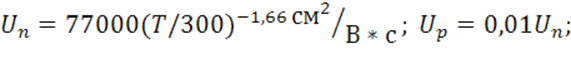
![]()
![]()
Найти: ![]() .
.
Решение:
Запишем уравнение электронейтральности, считая электронный газ невырожденным, а примесь – полностью ионизированной:
![]()
![]()
Сведём уравнение к квадратному и получим выражение для уровня Ферми:
![]()
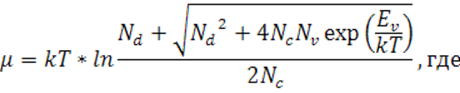
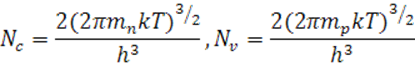
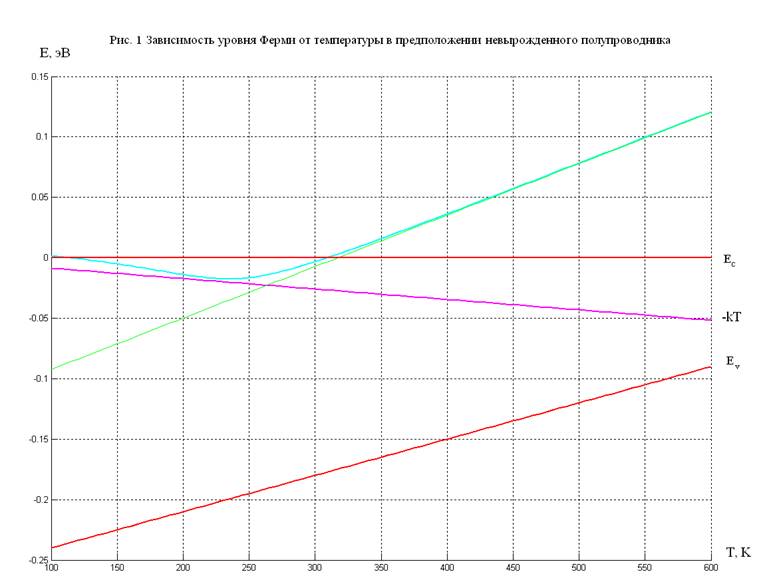
Из рис. 1 видно, что предположение о невырожденности
электронного газа в данном полупроводнике неверно, т.к. уровень Ферми
приближается много менее чем на ![]() дну зоны проводимости и даже частично находится в
зоне проводимости.
дну зоны проводимости и даже частично находится в
зоне проводимости.
Составим другое уравнение электронейтральности, используя приближенное выражение для концентрации вырожденного газа электронов в зоне проводимости:
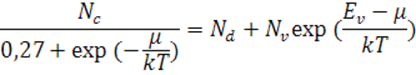
Оно также сводится к квадратному:
![]()
Получим выражение для уровня Ферми в вырожденном полупроводнике:
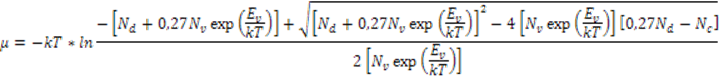
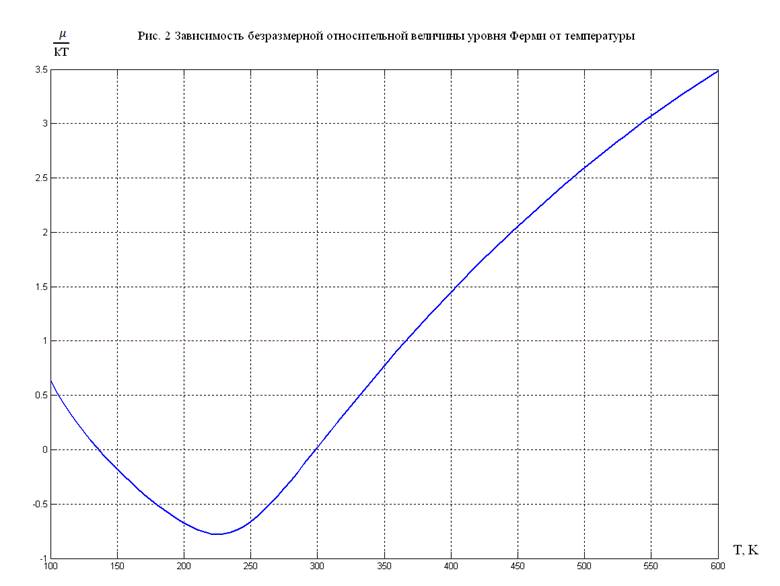
Приближенная
формула ![]() даёт малую ошибку только при
даёт малую ошибку только при ![]() Из рис. 2 видно, что такое
приближение верно только для
Из рис. 2 видно, что такое
приближение верно только для ![]() , поэтому при
, поэтому при ![]() будем использовать другое
приближение:
будем использовать другое
приближение:
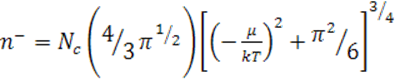 , верное при
, верное при ![]()
Получим
уравнение электронейтральности для температур ![]() :
:
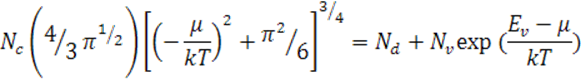
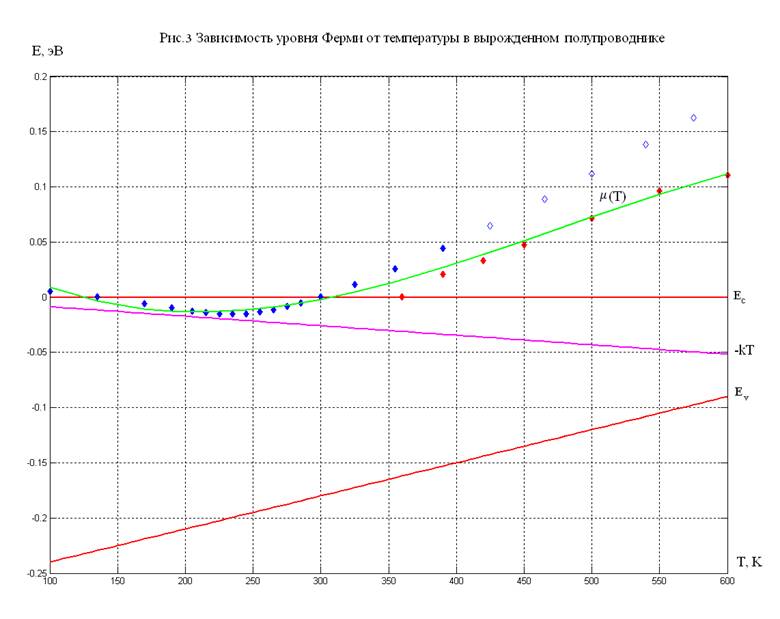
Оно не разрешимо в общем виде, но необходимое число опорных точек можно получить, используя численные методы, реализованные в вычислительной среде MatLab (см. рис. 3, красные ромбы). Выполняем “сращивание” двух участков кривой (синие и красные ромбы) и аппроксимацию полиномом третьей степени (зелёная кривая).
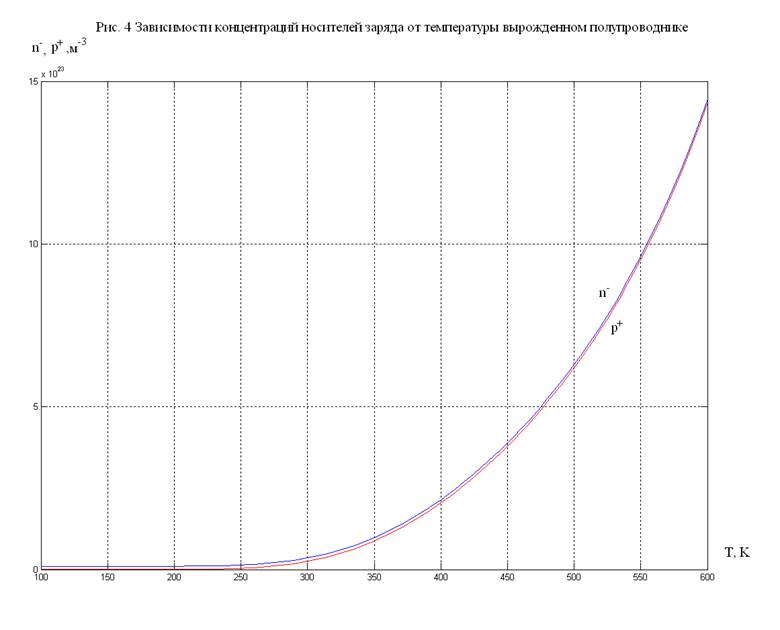
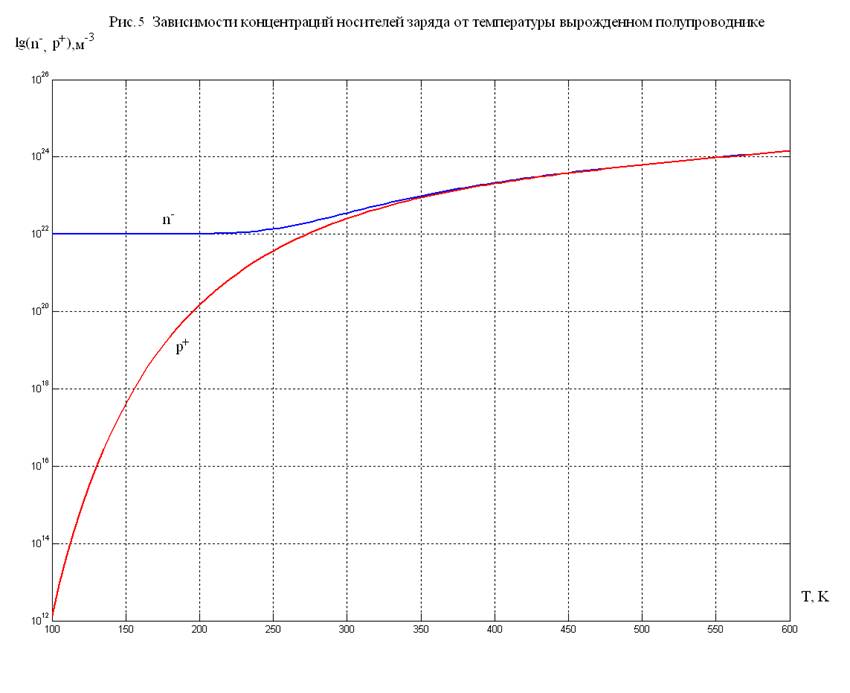
Далее,
получим зависимость концентрации дырок![]() и электронов
и электронов ![]() от температуры в линейном (см. рис. 4) и полулогарифмическом
(см. рис. 5) масштабах.
от температуры в линейном (см. рис. 4) и полулогарифмическом
(см. рис. 5) масштабах.
Используя выражение для электропроводности полупроводника:
![]() ,
,
получим
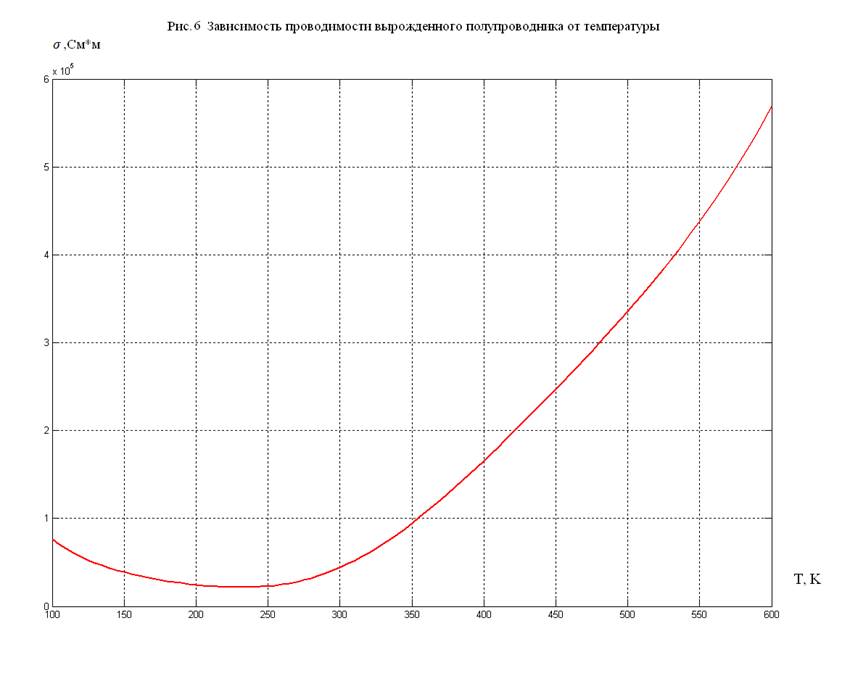
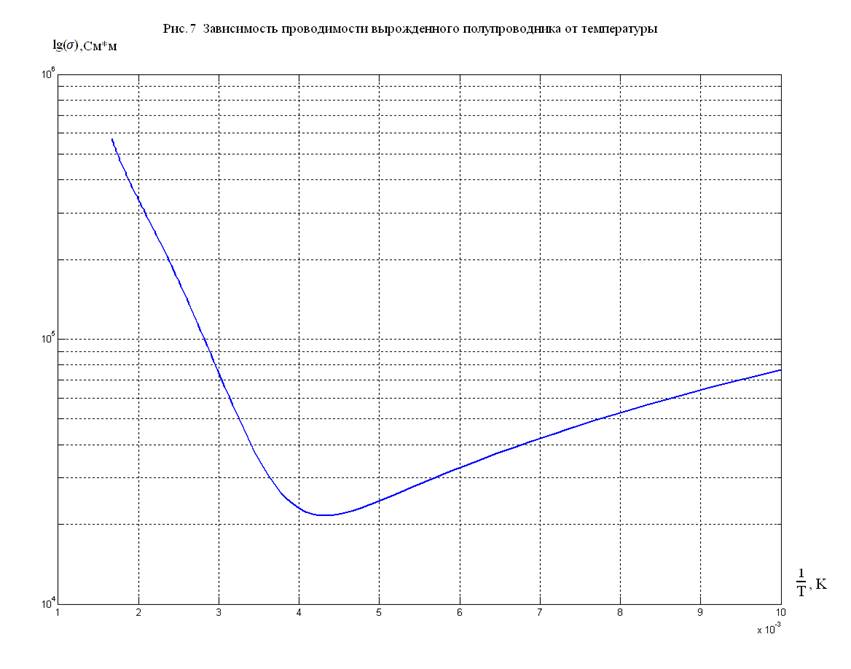
искомую кривую ![]() в линейном (см. рис. 6) и полулогарифмическом
масштабе (см. рис. 7).
в линейном (см. рис. 6) и полулогарифмическом
масштабе (см. рис. 7).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.