Временные диаграммы рис.4 отображают случай, когда комбинация <а4а3а2а1а0к> <101101> принимается без ошибок. Причем последовательность импульсов на выходе ДШПК соответствует передаче комбинации, начиная со старшего (а4) разряда. К моменту t2 подачи сигнала «РИ» на вход ДШ D4 в узлах фиксации УФК информационные элементы будут иметь установившиеся значения, а триггер D3 зафиксирует результат проверки. На диаграммах эти значения помечены крестиком X. И если триггер D3 в этот момент выдает сигнал лог.0, то на 24-м выходе D4 появится «расшифрованный сигнал». В момент t3 подается сигнал СБРОС, и схема возвращается в исходное состояние. Если у сумматора D1 (рис.3,а) или триггера D3 (рис.3,б) использовать инверсные выходы, то указанные схемы будут являться дешифраторами кода «нечет».
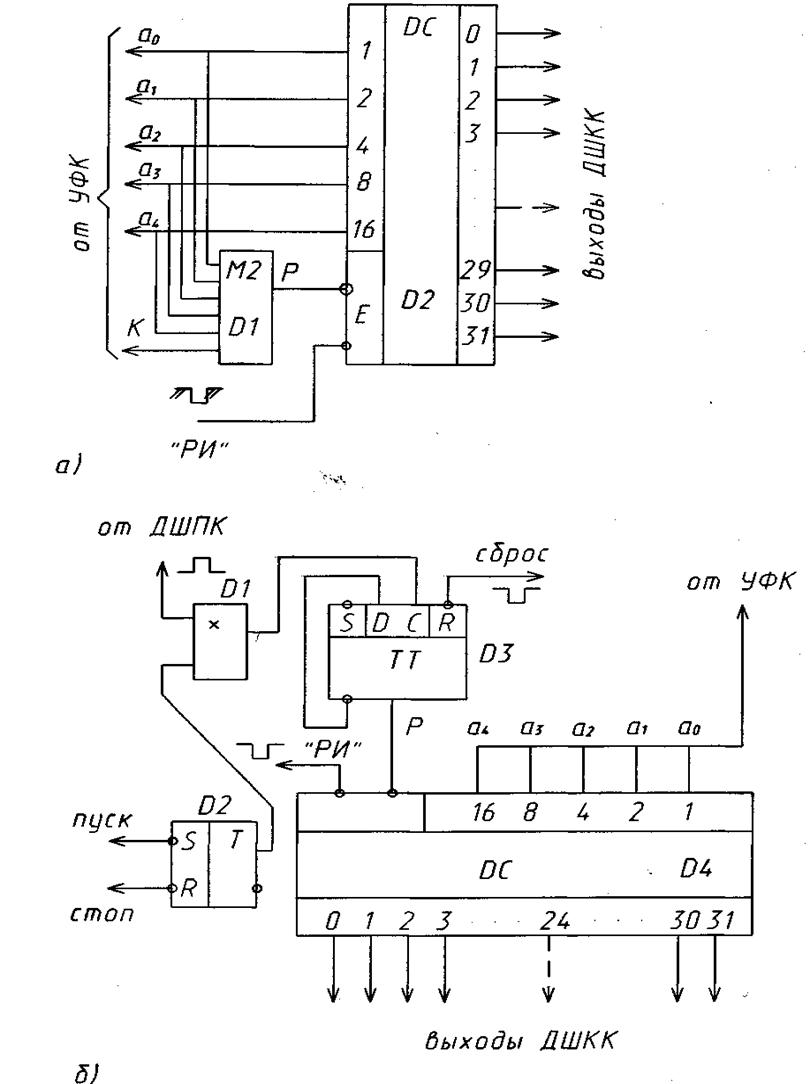
Рис. 3. Дешифраторы кода "чет-нечет":
а–комбинационный, б–последовательный
Рис. 4 Временные диаграммы к схеме рис. 3,б
Комбинационные ДШ кодов с коррекцией ошибок можно построить, зная правила формирования контрольных элементов и способ применения кода. Различают два способа применения: только для обнаружения ошибок и второй - для исправления ошибок.
В первом случае необходимо лишь выполнить регулярные проверки на четность и составить логическое условие, которое описывало бы сигнал «разрешения декодирования». Такие ДШ позволяют обнаружить r = d-1
ошибок, где d - минимальное кодовое расстояние.
Для реализации процедур исправления ошибок следует найти условия их опознавания в каждом информационном элементе комбинации - «опознаватель» ошибок. Затем составить логические выражения на исправление ошибок и на формирование сигнала «разрешение декодирования».
Покажем это для кода
Хэмминга, рассмотренного выше. Из выражений К1=а2
а1; К2=а2а0; КЗ=а1а0 и К0=К1а0 [2] вытекают
следующие проверки:
р0=
1ā2ā1; р1=2ā2ā0; р2=3ā1ā0; (2)
р=0ā2 (ā1ā03) 21=012ā2р2. (3)
Выражения (2) можно составить, пользуясь таблицей проверок (табл.2.3) и таблицей кодирования (табл.2.2) [2, с.52]. Если хотя бы одно из выражений (2), (3) примет значение лог.1, то в принятой комбинации есть ошибки. Таким образом, условие обнаружения ошибок имеет вид:
v=p2+pl+p0+p. (4)
Функциональная схема, соответствующая рассматриваемому варианту кодирования изображена, на рис.5. Для правильной работы ДШ (рис.5) в устройствах ТУ-ТС с последовательной передачей элементов комбинации сигнал «РИ» (разрешение исполнения ) должен подаваться лишь при синфазной работе распределителей ДП и КП.
Заметим, в системах с решающей обратной связью для «решения вопроса» о передаче сигналов ЗАПРОС, КВИТИРОВАНИЕ можно использовать сигнал v с выхода элемента D5 (рис. 5): если в момент подачи сигнала «РИ» v=0, то следует передать сигнал КВИТИРОВАНИЕ, а при v=l -сигнал ЗАПРОС.
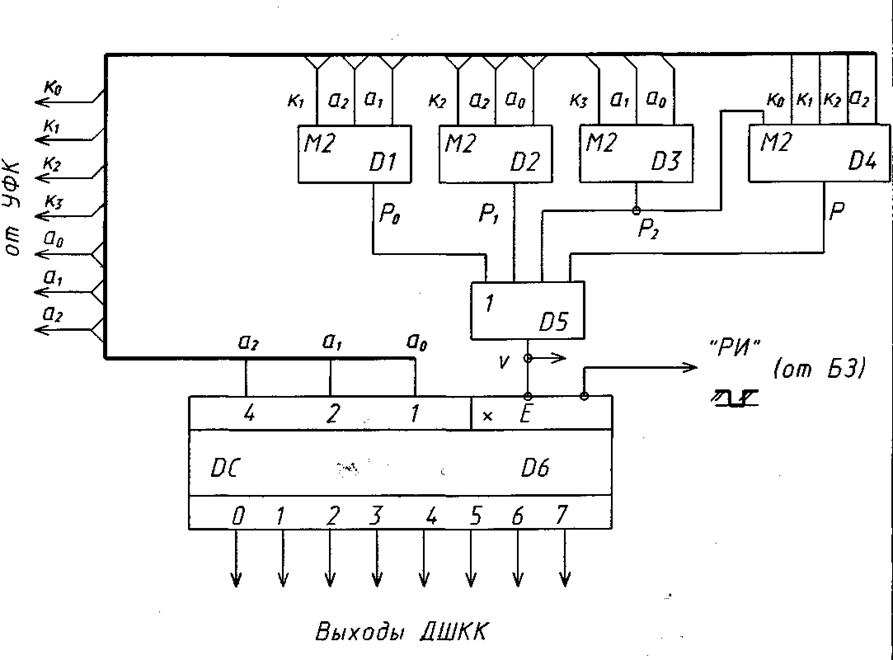
Рис. 5. Дешифратор кода Хемминга с d=4
и обнаружением 3 - х ошибок
Пользуясь рассмотренной методикой [2, с.54], нетрудно составить логические выражения для обнаружения ошибок в циклическом
(7,4 ) - коде:
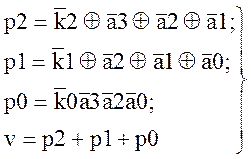(5)
Здесь, как в выражениях (2), (3), переменные со знаком (-) соответствуют зафиксированным на КП значениям элементов комбинации. Так как у этого кода 4 информационных, 3 контрольных элемента и минимальное кодовое расстояние d=3, то для построения декодирующего устройства потребуется один полный ДШ 4-го порядка, три 4-входовых сумматора по mod2 и один элемент ИЛИ (5). Такое устройство позволит обнаружить r=d-1=3-1=2 ошибки (любые) и некоторые 3-кратные ошибки. Например, ошибки в элементах а3, а2, a1 не нарушат проверки р1 и р0, но нарушают проверку р2, и, следовательно, будут обнаружены.
Исправление ошибок, как в кодах Хэмминга, так и в циклических кодах, можно реализовать, применяя единую методику отыскания опознавателей. Исходными данными, позволяющими отыскать опознаватели ошибок, служат логические выражения регулярных проверок на четность. В рассматриваемых примерах - это выражение (2) для кода Хэмминга и (5) для циклического (7,4) - кода. В общем случае, опознаватель ошибки - это результат проверок на четность, представленный в виде двоичного, так называемого проверочного числа. Причем опознаватель - это проверочное число, которое однозначно указывает позицию (знако-место), где возникла ошибка. Если декодировать комбинации, когда только по информационным элементам, то достаточно найти опознаватели ошибок этих элементов. В зависимости от числа исправляемых ошибок можно говорить об опознавателях одиночных, двойных и большей кратности ошибок. Однако при попытках отыскать опознаватели ошибок, кратность которых превышает допустимую, получатся неразличимые опознаватели.
Найдём опознаватели (одиночных) ошибок для кода Хэмминга, рассматриваемого в качестве примера. Для этого результаты проверок (4) будем записывать в виде двоичного числа <p2p1p0>, где р2 - результат 3-й проверки (старший разряд проверочного числа), а р0 -самый младший разряд проверочного числа и результат 1-й проверки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.