




























КОМПЛЕКСНАЯ КУРСОВАЯ РАБОТА
|
На тему |
Транспортная задача перевозки неоднородного груза |
|||
|
Студент |
А |
|||
|
подпись |
дата |
инициалы, фамилия |
||
|
Группа |
9ПО091 |
|||
|
Специальность |
Программное обеспечение вычислительной техники и автоматизированных систем |
|||
|
шифр, название |
||||
|
Руководители |
|
|||
|
подпись |
дата |
инициалы, фамилия |
||
|
|
||||
|
подпись |
дата |
инициалы, фамилия |
||
БАРНАУЛ 2012
Содержание.. 2
Введение.. 3
Сущность математического метода.. 5
1 Характеристика метода перевозки неоднородного груза. 5
2 Аналитическое решение задачи перевозки неоднородного груза 11
Анализ и уточнение требований к программе.. 15
1 Анализ процесса обработки информации и выбор структур данных для ее хранения. 15
4 Разработка основных алгоритмов решения задачи. 17
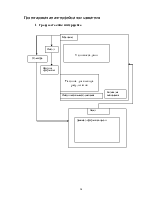
Проектирование интерфейса пользователя.. 19
1 Граф состояния интерфейса. 19
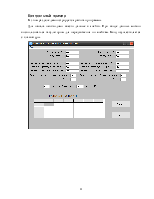
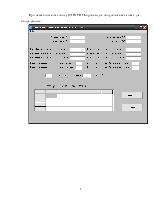
2 Формы ввода-вывода информации. 20
Контрольный пример. 22
Заключение.. 26
Список литературы... 27
Приложение A.. 28
Тема курсовой работы – транспортная задача перевозки неоднородного груза.
Транспортная задача является разновидностью линейного программирования. Возникновение и развитие линейного программирования связано с экономикой. В экономике задачи математического программирования, и в частности линейного, возникают в связи с многочисленностью вариантов создания или функционирования определенной экономической системы, с возможностью применения различного сырья, материалов, технологии для производства одной и той же продукции.
Линейное программирование является наиболее развитым и широко используемым на практике разделом математического программирования. Предложение о линейности экономических зависимостей несколько ограничивает возможности линейного программирования, однако простота и наглядность линейных моделей, с достаточной степенью точности описывающих экономические процессы, позволяет применять эти модели в различных видах экономической деятельности.
Основы линейного программирования были заложены советским математиком Л.В. Канторовичем в конце 30-х годов.
В 1949 г. Л.В.Кантоновичем и М,К. Гавуриным предложен новый точный метод для решения транспортной задачи – метод потенциалов. В последующие годы вклад в развитие теории линейного программирования внесли ученые многих стран мира.
Цель данной работы заключается в создании программного продукта для решения задач по теме: «Транспортная задача перевозки неоднородного груза».
Задачи курсовой работы:
- изучить теоретический материал по данной теме;
- изучить методы решения задач;
- создать алгоритм для решения данной задачи;
- создать программу для решения задач данного класса.
Программа будет разработана в среде Delphi.
Системные требования: Win 98/SE/2000/ME/XP, 256 RAM.
Иногда встречаются задачи перевозки неоднородного груза к таким, например, относится планирование перевозок угля разных сортов, цемента разных марок, сортового железа и т.д. Характерной чертой всех этих задач является условие взаимозаменяемости различных сортов перевозимого груза при удовлетворении потребностей. Это означает, иными словами, что некоторая часть потребностей может быть удовлетворена различными видами имеющегося в наличии груза и характера потребностей. Мы рассмотрим, каким образом подобные задачи могут быть приведены к задачам о перевозках некоторого условного однородного груза.
Пусть, например, имеются два поставщика – А1и А2 и два потребителя В1и В2.
У каждого поставщика имеется груз двух сортов (например, бурый уголь и антрацит, цемент марок 500 и 600 и т.д.). Обозначим ресурсы 1-го поставщика по каждому из сортов груза через а11 и a111 и аналогично, 2-го поставщика – через а12 и a112.
В дальнейшее мы будем рассматривать не два, а как бы четыре поставщика, ресурсы которого соответственно равны а11, а111, а12 и а112. Теперь перейдем к анализу потребностей каждого потребителя. Очевидно, в условиях данной задачи эти потребности у каждого потребителя могут быть трех видов.
1 Потребности только на первый сорт груза. Обозначим их соответственно для 1-го потребителя через b11и для второго через b12.
2 Потребности только на второй сорт груза (соответственно b111и b112).
3 Взаимозаменяемые потребности на любой из сортов груза (соответственно b1111и b1112).
Будем полагать, что b1111и b1112означают потребности 1-го и 2-го потребителя, выраженные в единицах первого сорта груза.
Вместо каждого из двух потребителей В1 и В2 будем в дальнейшем рассматривать три потребителя с потребностями b1, b11 и b111.
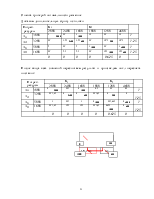
Занесем все перечисленные исходные данные и, кроме того, коэффициенты затрат Cik на перевозку единицы груза в таблицу №1.
Оформление таблицы в методичке
Таблица 1
b11 a11 |
B1 |
B2 |
||||
|
b11 |
b111 |
b1111 |
b12 |
b112 |
b1112 |
|
|
a11 |
c11 |
c11 |
c11 |
c12 |
c12 |
c12 |
|
a111 |
c11 |
c11 |
c11 |
c12 |
c12 |
c12 |
|
a12 |
c21 |
cc1 |
c21 |
c22 |
c22 |
c22 |
|
a112 |
c21 |
c21 |
c21 |
c22 |
c22 |
c22 |
Будем полагать, что коэффициенты затрат от сорта перевозимого груза, а определяются только тем, «откуда» и «куда» он перевозится.
Пусть p - единицы груза первого сорта могут
быть замены при удовлетворении 3-й категории потребностей q – единиц второго сорта. Тогда
отношение ![]() назовем коэффициентом
взаимозаменяемости. Он показывает, сколько единиц груза второго сора могут
заменить
назовем коэффициентом
взаимозаменяемости. Он показывает, сколько единиц груза второго сора могут
заменить
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.