Проверка показала, что найденный элемент является искомым
2.7. Найти порядок элемента λ(α).
α7 = α3 + 1
α8 = α4 + α
α9 = α5 + α2
α10 = α6 + α3
α11 = α4 + α3 + 1
α12 = α5 + α4 + α
α20 = (α6 + α3) * (α6 + α3) = α12 + α9 + α9 + α6 = α6 + α5 + α4 + α
α40 = (α6 + α5 + α4 + α)*( α6 + α5 + α4 + α)= α12 + α11 + α10 + α7 + α11 + α10 + α9 + α6 + α10 + α9 + α8 + α5 + α7 + α6 + α5 + α2 = α6 + α5 + α3 + α2
α80 = ( α6 + α5 + α3 + α2)*( α6 + α5 + α3 + α2) = α5 + α3 + α
α89 = ( α5 + α2)*( α5 + α3 + α) = α5 + α4 + α3 + α + 1
λ(α) = α89
2.8. Найти в какой степени элемент αс станет равным элементу α
αс = α8= α4 + α
(α8)2 = α4 + α2 + α
(α8)4 = α2 + α
(α8)8 = (α8)4 * (α8)4 = α4 + α2
(α8)16 = (α8)8 * (α8)8 = α
Ответ: в 16 степени.
Задание 3.
sn+b = sn+b-2 + sn
sn+5 = sn+3 + sn
3.1. Нарисовать электронную схему последовательности.
 |
3.2.Найти характеристический многочлен последовательности и разложить его на множители.
Sn+5 = Sn+3 + Sn
Sn+5 – Sn+3 – Sn = 0
В таком случае характеристическое уравнение будет иметь вид:
x5 – х3 – 1 = 0
Вероятнее всего (учитывая последующие задания и использование регистров сдвига для моделирования последовательности), все вычисления проводятся не в поле действительных (или комплексных) чисел, а в поле GF(2k+1), то есть в поле GF(26). В задании явно не указано, в каком поле проводить вычисления. Данный многочлен имеет в поле действительных чисел 1 корень, и 4 корня в поле комплексных чисел. Решение последующих заданий (а именно 3.4, 3.5, 3.6) возможно только в поле GF(26), поэтому дальнейшее решение будет представлено для этого поля.
В таком случае характеристическое уравнение примет вид:
x5 + х3 + 1 = 0
Этот элемент и будет неприводимым над полем GF(26).
3.3.Найти явную формулу для n-го члена рекуррентной последовательности.
Явная формула для n-го члена рекуррентной последовательности:
Sn
= β1![]() +
β2
+
β2![]() +
β3
+
β3![]() +
β4
+
β4![]() +
β5
+
β5![]() +
β6
+
β6![]()
Где α1, α2, α3, α4, α5, α6 – корни характеристического уравнения. В поле GF(26) характеристическое уравнение решений не имеет, следовательно невозможно записать явное уравнение n-го члена через формулу. Для поля комплексных чисел, где могут быть найдены корни уравнения х5 – х3 - 1 = 0, можно записать явную формулу n-го члена. Корни уравнения будут:
α1 = 1,24
α2 = -0,96 + 0,43i
α3 = -0,96 - 0,43i
α4 = 0,34 – 0,79i
α5 = 0,34 + 0,79i
Среди корней отсутствуют кратные, значит явная формула n-го члена примет общий вид:
Sn = ![]()
β1, β2, β3, β4, β5 находятся при решении системы уравнений:
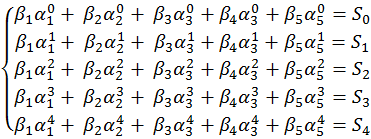
Решить эту систему не представляется возможным, так как не известны первые k членов последовательности (S0, S1, S2, S3, S4) – вектор инициализации. Явная формула n-го члена последовательности в таком случае будет иметь вид:
Sn = 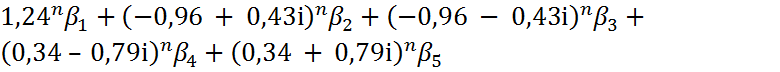
3.4.Найти период последовательности «в лоб»
000001 - шаг 1
000010 - шаг 2
000100 - шаг 3
001001 - шаг 4
010010 - шаг 5
100100 - шаг 6
001000 - шаг 7
010000 - шаг 8
100000 - шаг 9
000001 - шаг 10
В теоретическом материале было указано, что наибольший период получается при векторе инициализации (0, 0, 0, 0, 0, 1). Такой вектор называется импульсной функцией. При использовании данного вектора инициализации, период получается равен 10, что не является наибольшим возможным периодом для данного регистра сдвига (26-1).
3.5.Найти, в какой степени матрица последовательности станет равной единичной.
Предположим, что начальное состояние последовательности (0, 0, 0, 0, 0, 1).
Матрица при данных начальных условиях будет иметь вид:
A
= 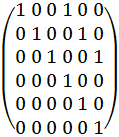
Найдем степень, в которой матрица А станет равной единичной, то есть Аm = E
A2 = 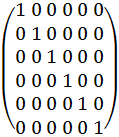
При возведении в квадрат, матрица становится единичной.
3.6.Найти в какой степени элемент α станет равным 1
Элемент α в нашем регистре будет иметь запись (0, 0, 0, 0, 0, 1, 0)
Элемент 1 в нашем регистре будет иметь запись (0, 0, 0, 0, 0, 0, 1)
Следовательно, надо найти на каком шаге регистр, при векторе инициации α даст 1. Учитывая, что период последовательности = 10, а элемент α следует сразу же за элементом 1, можно утверждать что α9 = 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.