1.5. В поле GF(pn) решить систему линейных уравнений
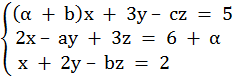
Учитывая, что:
а – количество букв в фамилии (Яресько) = 7 (mod 5) = 2
b – количество букв в имени (Антон) = 5 (mod 5) = 0
с – количество букв в отчестве (Павлович) = 8 (mod 5) = 3
Система уравнений приобретает вид:
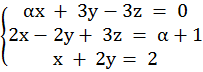
Решение:
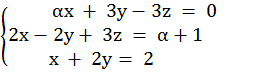
Складываем вторую и первую строки:
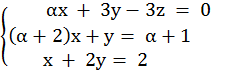
Отдельно решим систему, состоящую из второго и третьего уравнения(система 2):
![]()
Из второго уравнения второй системы:
x=2+3y
Подставляем в первое уравнение второй системы и получаем:
![]()
![]()
![]()
![]()
Выражаем из полученного y x:
![]()
Выражаем из первого уравнения первой системы z:
![]()
![]()
Ответ:(![]() ;
;![]() ;
;![]() .
.
1.6. В поле GF(pn) найти элемент обратный по умножению к α + c (mod p) при помощи примитивного элемента и перепроверить по методу Евклида.
α + с = α + 3
(α + 3)-1 = 4α2 + 3α + 3
Проверка алгоритмом Евклида:
f(α) = α3 + 3α + 2
g(α) = α + 3
f(α) = (α2+2α) * g(α) + (2α+2)
g(α) = 3*(2α+2) + 2
2 = g(α) - 3*(2α+2)
(2α+2)= f(α)- g(α)*( α2+2α)
1=(2-1)*(g(α)- 3*(2α+2))= (2-1)*(g(α)- 3*( f(α)- g(α)*( α2+2α)))= (2-1)*( g(α)- 3f(α)+g(α)*( 3α2+α))= (2-1)*( 2f(α)+g(α)*( 3α2+α+1))=3*( 2f(α)+g(α)*( 3α2+α+1))=0+g(α)*( 4α2+3α+3)=g(α)*( 4α2+3α+3)=>g-1(α)= 4α2+3α+3
Ответ:( 4α2+3α+3).
1.7. В поле GF(pn), используя примитивный элемент и логарифм Якоби, решить систему уравнений
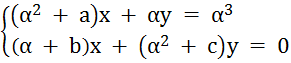
При а = 7, b = 5, c = 8, система приобретает вид:
![]()
Выразим y из второго уравнения системы:
![]()
![]()
![]()
![]()
Подставим y в первое уравнение системы:
![]()
![]() Прим.:
Прим.:![]()
![]()
![]()
![]()
![]()
![]()
Подставляем в y:
![]()
Ответ:![]() ).
).
1.8. По формуле быстрого возведения в степень вычислить αb+c (mod 701).
α 5+8 = α13 = α * α4 * α8
Нам дано поле 701. Так как число 701 не является степенью какого-либо простого числа, то это поле нельзя назвать расширенным полем. Вследствие чего можно сказать, что примитивный элемент α будет весьма конкретным, а именно:
α = 2
α2 = 4
α4 = 16
α8 = 256
α13 = α * α4 * α8 = 2 * 16 * 256 (mod 701) = 481
Задание 2.
2.1. Над полем GF(2) методом Гаусса найти определитель матрицы А размера n x n, состоящей из младших разрядов двоичного разложения числа abс, сдвинутого циклически.
abc=280
abc = 100011000
Берём последние три цифры и сдвигаем число циклически влево, повторям операции.
А
= 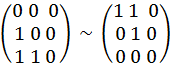
|A| = 1 * 1 * 0 = 0
2.2. Методом Гаусса найти характеристический многочлен матрицы А.
Характеристический многочлен f(λ):
f(λ)
= |A - λE|
= 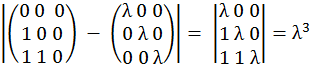
2.3. Разложить многочлен f(λ) над полем GF(2) на неприводимые множители и найти его корни.
f(λ) = λ3 = 0
λ3 = 0
λ =0
Ответ: 0.
2.4. Найти собственные вектора для всех собственных значений матрицы А.
А = 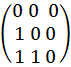
Определим координаты собственного вектора:
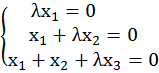
![]() =
λ3
=
λ3
Находим корни:
λ3=0
λ = 0
Подставляем в систему:
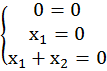
![]()
Ранг матрицы системы линейных уравнений = 2, следовательно, зависимых переменных две, свободная одна.
Пусть ![]() –
свободная переменная, тогда:
–
свободная переменная, тогда:
![]()
![]()
Ф.С.Р:
![]()
Таким образом, все собственные векторы матрицы А:
(0, 0, 1), (0, 0, 0)
2.5. Разложить на неприводимые множители над полем GF(2) многочлен f(x).
Дано задание, но не дан многочлен для разложения.?
2.6. Найти элемент, обратный по умножению
к элементу ![]() в
поле GF(27).
в
поле GF(27).
λ(α) = α7 + α5 + α8
Построим поле, используя элемент α7 + α3 + 1
f(x) = x7 + x3 + 1
f(x) ≠ 0
f(α) = 0
α7 + α3 + 1 = 0
α7 = α3 + 1
α8 = α4 + α
α9 = α5 + α2
Элемент, которому ищем обратный, будет иметь вид:
λ(α) = α7 + α5 + α8 = α5 + α4 + α3 + α + 1
Найдем обратный, используя алгоритм Евклида:
f(α) = (α2 + α) * λ(α) + (α4 + α + 1)
λ(α) = (α + 1) * (α4 + α + 1)+ (α3 + α2 + α)
(α4 + α + 1)= (α + 1) * (α3 + α2 + α)+ 1
1 = (α4 + α + 1) + (α + 1) * (α3 + α2 + α)= (α4 + α + 1)+ (α + 1) *[ λ(α)+ (α + 1) * (α4 + α + 1)]= (α4 + α + 1)+ (α + 1) * λ(α)+( α2 + 1)*( α4 + α + 1)=( α4 + α + 1)* α2+(α + 1) * λ(α)= α2*(f(α) + (α2 + α) * λ(α)) + (α + 1) * λ(α) = α2*f(α) + (α4 + α3)*λ(α)+ (α + 1) * λ(α) = α2*f(α) + λ(α) * (α4 + α3 + α + 1) = 0 + λ(α) * (α4 + α3 + α + 1) = (λ(α))-1 * λ(α)
Обратный по умножению для α5 + α4 + α3 + α + 1 будет α4 + α3 + α + 1
Проверка:
(α5 + α4 + α3 + α + 1) * (α4 + α3 + α + 1) = α9 + α8 + α6 + α5 + α8 + α7 + α5 + α4 + α7 + α6 + α4 + α3 + α5 + α4 + α2 + α + α4 + α3 + α + 1= α9 + α5 + α2 + 1= α5 + α2 + α5 + α2 + 1 = 1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.