Планирование и организация экспериментов. Обоснование и описание методов оптимизации. Метод Гаусса-Зайделя. Метод поиска с «наказанием случайностью»

Эксперимент может быть завершен, так как не наблюдается изменения критерия оптимальности и ни по одной из переменных не удается получить лучшее значение, следовательно, данная точка является решением поставленной задачи.

Для того чтобы определить является ли найденный экстремум локальным или глобальным, возьмем новую начальную точку  с координатами (-1;-1;0;0;-1;    -1) и значением критерия Уср=4,02 и заново проведем поиск.

Таблица 3 – Цикл первый, h=1

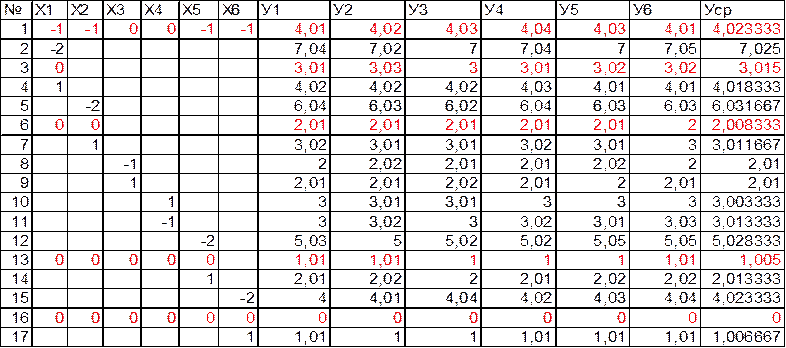
Проверим на следующем этапе с меньшим шагом не является ли полученная точка искомым экстремумом.

Таблица 4 – Цикл второй, h=0,5

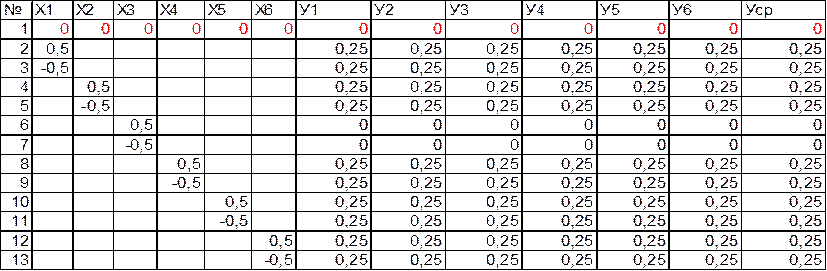
Эксперимент может быть завершен, так как не наблюдается изменения критерия оптимальности и ни по одной из переменных не удается получить лучшее значение. Точка полностью совпала с той, которая получена вначале. Поэтому можно сделать вывод о том, что полученный минимум является глобальным.

2.2  Метод поиска с  «наказанием случайностью»

Из начальной точки (2;2;1;1;2;2) с Уср =12,50    ищем минимум критерия оптимальности. Серия неудачных попыток =8.

Таблица 5 – Поиск точки с минимумом критерия оптимальности

Получили лучшую точку (0;0;0;0;0;0), значение критерия Уср=0. Эксперимент может быть завершен, так как за заданное число попыток невозможно получить лучшей точки. Поэтому полученная точка будет являться решением задачи.

Для того чтобы определить является ли найденный экстремум локальным или глобальным возьмем новую начальную точку и заново проведем поиск.

Из новой точки ( -1; 1; -2; -1; -2; -1) с Уср =5,30   ищем минимум критерия оптимальности. Серия неудачных попыток =8.

Таблица 6 – Поиск точки с минимумом критерия оптимальности

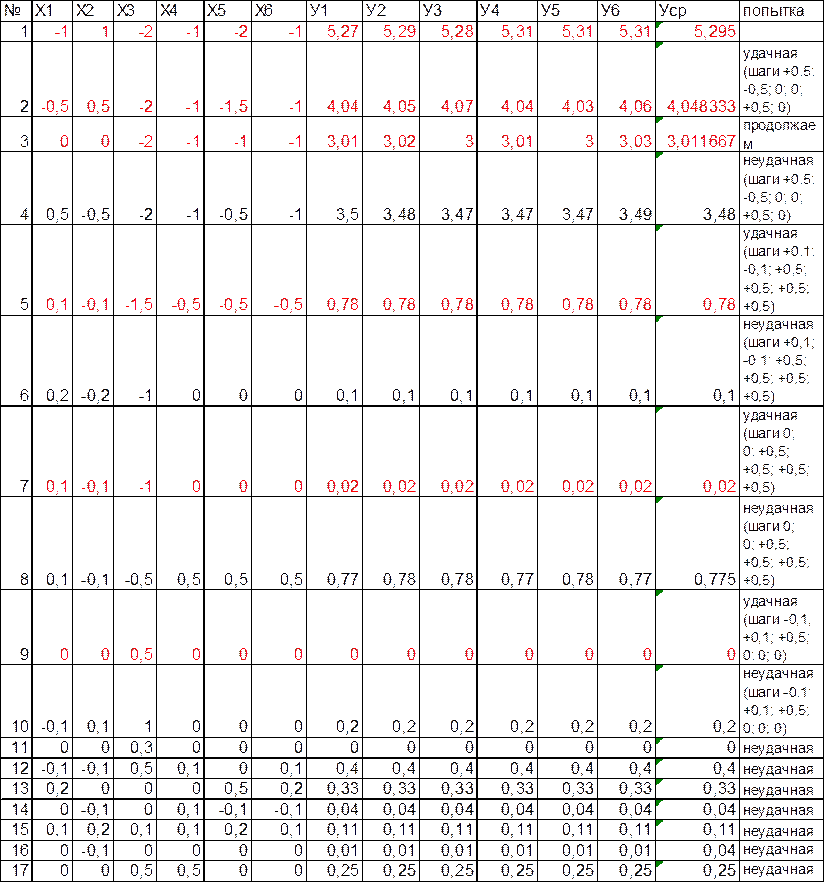
Получили лучшую точку (0;0;0,5;0;0), значение критерия Уср=0. Эксперимент может быть завершен, так как за заданное число попыток невозможно получить лучшей точки. Точка практически совпала с той, которая получена вначале этим методом. Поэтому можно сделать вывод о том, что полученный минимум близок к глобальному.

После проведения поисков двумя различными методами получили практически один результата. Следовательно, можно сделать вывод о том, что найденный минимум наиболее близок к глобальному.

3.Подбор реального процесса

Необходимо подобрать реальный процесс с  шестью влияющими входными переменными.

Рассмотрим технологический процесс резиносмешения, оптимизация которого позволит получить нужный уровень условной прочности резины при растяжении (кгс/см² или Н). Факторы, влияющие на процесс:

1.  Количество технического углерода, г

(Оптимальная степень наполнения для каждого вида каучука своя. Для каучука СКИ-3 количество ТУ выше, для каучука НК ниже. Если ниже и выше оптимальные значения ТУ, то уровень прочности ниже. Тоже для НК, высокая навеска, то все количество ТУ не  вотрется в каучук и прочность будет низкая. Если низкая навеска ТУ, ниже оптимального значения, то количество ТУ будет недостаточно для усиления каучука, значит прочность будет низкой);

2.  Уровень модуля 300%, кгс/см² или Н

(Определяется навеской серы и ускорителя, значение навески варьируют и меняют  влияющие параметры в компьютере. Это уловное напряжение при 300% удлинения (гостированный показатель для резиновой смеси). Чем выше уровень модуля, тем выше прочностные характеристики, для высокого модуля навески серы и ускорителя высокие);

3.  Температура процесса, ^оС

(в резиносмесителе существуют две термопары: в стенке и на нижнем затворе, температура устанавливается в компьютере в зависимости от вида каучука, например, для натурального или СКИ-3 – не выше 140^оС. При повышении температуры выше 140 ^оС происходит структурирование