Исследование свойств линейной электрической цепи постоянного тока, страница 2

 I₃^’’-I₅^’’-I₆^’=0;                     0,25-0,12-0,14=-0,01.

      По  принципу  наложения  токов, имеем:

      I₁=I₁^’- I₁^’’                            0,44=0,65-0,2;

      I₂=-I₂^’+I₂^’’                           0,25=-0,2+0,45;

      I₃=I₃^’+I₃^’’                            0,66=0,42+0,25;

      I₄=-I₄^’+I₄^’’                          0,1=-0,25+0,35;

      I₅=I₅^’+I₅^’’                            0,17=0,05+0,12;                            

      I₆= I₆^’+I₆^’’                            0,5=0,4+0,14; 

При исследовании законов Кирхгофа   мы  убедились в их справедливости для электрических цепей постоянного тока.

          Вывод: Мы изучили и экспериментально проверили одно из основных свойств линейных цепей; принцип наложения для напряжения и токов; абсолютная погрешность полученная в результате экспериментов не превысила допустимые значения.

Задание №2.

              Линейные соотношения  в электрических цепях.

 Измерим   следующие  токи  и запишем их  значения  в таблицу 3.

                                                                                                           Таблица 3

Значение переменного параметра R5	I2,mA	I3,mA
R5 min	0,	0,8
R5  ср	0,15	0,5
R5 мах	0,05	0,25

    Для  нахождения  линейного  соотношения    I₂=a+bI₃   собирём  следующию  схему.

 

                                                          л                                                            

                                                           R₂                                                        

                                                                                      л

                             +                           п  

                 E₁                                                         R₃                               

                              -                                                       п

                                л                                                                      

                R₅                                                                                                                      

                               п                        в                             в              

                                                    mA₂                               mA₃

                           в                             н                          н    

                     mA₅                                                                                                           

                            н

                                                  схема  5.                                        

      Исходя  их  наших  измерений  и  схемы, получим:

          I_2min=а+bI_3min ;                    

          I_2max=a+bI_3max;

          I_2ср=a+bI_3ср;

       Найдём  значения  a, b, решив  предыдущею  систему:       

          0,2=a+0,8b ;              а=0,2-0,8b ;                    а=0,2-0,8b;                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                           

          0,05=a+0,25b;           0,05=a+0,25b;               0,05=0,2-0,8b+0,25b;

 

         а=0,2-0,8b;                а=-0,0182;                                                              

        -0,15=-0,55b;             b=0,2727;

            Проверка:

      0,05=-0,0182+0,25 0,2727;

      0,05=0,049-верно.

      Тогда  уравнения   принимают  вид:                                      

      I_2min=-0,0182+0,2727I_3min ;

      I_2max=-0,0182+0,2727I_3max;

      I_2ср=-0,0182+0,2727I_3ср;

     Построим  график  функции  I_2ср=f(I_3ср),получим  рис 1.(см.  в  конце)

Вывод: входе  выполнения  данного  задания, мы  изучили  и  проверили  принцип  линейности. Абсолютная  погрешность  в  данном  случае  не  превысила  допустимые  значения.

Задание №3

  Входные и взаимные проводимости ветвей. Изучение принципа взаимности.

Все значения  измеренных токов  запишем в таблицу 4.

                                                                                                               Таблица 4.

Номер ветви  в которую включается ЭДС	Токи   ветвей,       (mА)
	I1	I2	I3
I	0,65	0,15	0,5
II	0,15	0,65	0,5
III	0,5	0,5	1

E=11В

          Определим  все  входные  проводимости   по  формуле:   ,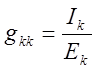

 а  также  все  взаимные  проводимости  ветвей:   .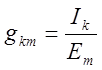

g₁₁=0,65А/11В=0,06См;

g₁₂=0,15А/11В=  0,014См;

g₁₃=0,5А/11В=0,045См;

g₂₁=0,15А/11В=0,014См;

g₂₂=0,65А/11В=0,06См;

g₂₃=0,5А/11В=0,045См;

g₃₁=0,5А/11В=0,045См;

g₃₂=0,5А/11В=0,045См;

g₃₃=1А/11В= 0,09См;

     По  полученным  значениям  проводимостей  составим  матрицу.

 

             0,06   0,014   0,045           

[g]=      0,014   0,06   0,045

             0,045  0,045   0,09

   Исследование теоремы об эквивалентном генераторе.

Соберем следующию  схему:

                                                                                                                      I₂                                                                       Е₁                                                                                                                                                                                                                                                                                                                               E   E_Э2=U_xx                                                            R₅                        

                   R₂                   R₃                                                                                                             R₂

                                                                                    R_вн.=R_вх.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                               

Для  того, чтобы  найти  I₂  воспользуемся  следующей  формулой:

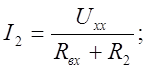 где

                

                

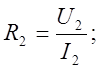
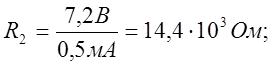
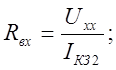
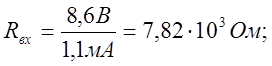
       Отсюда, получим, что:

 

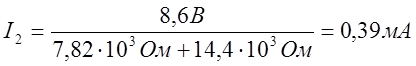
Вывод: при  выполнении  данного  задания, мы  изучили  и  проверели  одно  из основных  свойств  линейной  электрической  цепи: метод  эквивалентного  генератора.

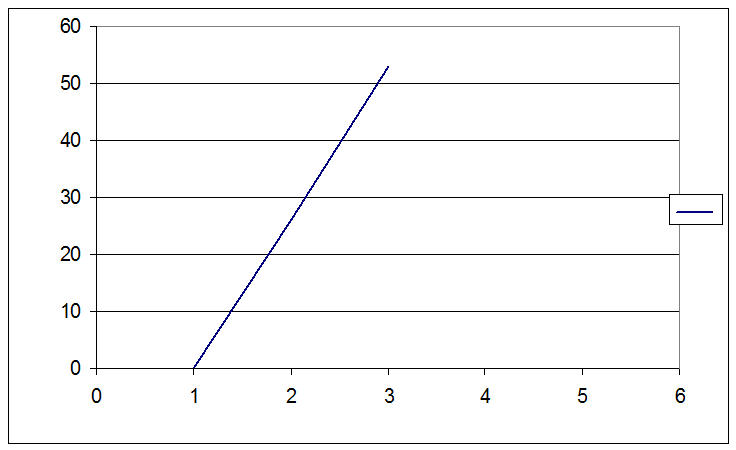                                                                         Рис 1.