косозубых колес расчетное допускаемое контактное напряжение
[σН]=0,45([σН1] + [σН2] ),(п.1, формула 3.10)
где: [σН1] – расчетное контактное допускаемое напряжение для шестерни;
[σН2] - расчетное контактное допускаемое напряжение для колеса.
Для шестерни:
![]()
![]() МПа.
МПа.
для колеса :
![]() МПа.
МПа.
[σН] =0,45([σН1] + [σН2])=0,45(555+427)=442МПа.
Требуемое условие [σН]≤1,23[σН2]=1,23·427=525 МПа 442 МПа< 525 МПа выполнено.
|
2.2 Определение межосевого расстояния |
Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев
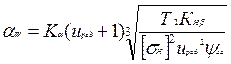 [п.1,
формула 3.7.) ]
[п.1,
формула 3.7.) ]
где: Кα – вспомогательный коэффициент. Для косозубых передач = 43,0.
KHβ –коэффициент неравномерности нагрузки по длине зуба. Для передач с симметричным расположением колес по отношению к опорам = 1,0
[п.1, таблица 3,5]
ψba – коэффициент ширины зубчатого венца. Для косозубых колес принимаем = 0,4.
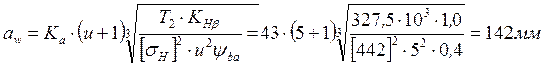
Принимаем стандартное значение межосевого расстояния aw =140 мм. [п.1,стр.36]
|
2.3 Определение нормального модуля зацепления |
![]()
![]() Модуль передачи
Модуль передачи
![]()
![]() =(0,01...0,02)140=1,4...2,8
мм.
=(0,01...0,02)140=1,4...2,8
мм.
Принимаем стандартное значение модуля mn =2 мм. [п.1,стр. 36]
|
2.4 Определение числа зубьев шестерни и колеса |
Принимаем предварительно угол наклона зубьев β = 10о и определяем числа зубьев шестерни и колеса
![]() [п.1, формула
3.16.]
[п.1, формула
3.16.]
Принимаем z1 =23.
z2 = z1 uред = ![]() =115.
=115.
Уточненное значение угла наклона зубьев
![]()
![]()
|
2.5 Определение основных размеров шестерни и колеса |
Диаметры делительных окружностей:
Шестерни
![]() мм;
мм;
Колёса
![]() мм.
мм.
Проверка межосевого расстояния:
![]() мм, что
соответствует определённому ранее значению.
мм, что
соответствует определённому ранее значению.
Диаметры окружностей вершин зубьев:
Шестерни
![]() мм;
мм;
Колёса
![]() мм.
мм.
Диаметры окружностей впадин зубьев:
Шестерни
![]() мм
мм
Колёса
![]() мм
мм
Ширина колеса ![]() ,
принимаем b2=56 мм.
,
принимаем b2=56 мм.
Ширина шестерни ![]() =56+4
мм=60 мм.
=56+4
мм=60 мм.
Коэффициент ширины шестерни по диаметру ![]()
Окружная скорость колес и степень точности передачи:
![]()
При такой скорости для косозубых колес следует принять 8-ю степень точности (п.1, стр. 32).
Силы в зацеплении:
Окружная
![]() Н;
Н;
радиальная
![]() ;
;
осевая
![]()
![]() Н.
Н.
2.6 Проверка контактных напряжений
Проверочный расчёт на контактную прочность проводиться по формуле:
![]() [п.1,
формула 3,6]
[п.1,
формула 3,6]
где: KH – коэффициент нагрузки;
Коэффициент расчётной нагрузки при расчёте на контактную прочность
KH= KHβ KHα KHυ,
где: KHα – коэффициент. Учитывающий распределение нагрузки между зубьями колес.
( При υ≤5 м/с и 8-й степени точности KHα = 1,08) [п.1, таблица 3,4]
KHυ – коэффициент динамической нагрузки.
(Для косозубых передач при υ≤5 м/с KHυ =1,0 [п.1, таблица 3,6]
Значение ![]() было
найдено при расчёте межосевого расстояния.
было
найдено при расчёте межосевого расстояния.
Таким образом, KH= 1·1,08·1 = 1,08
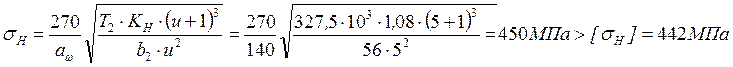
Перегруз составляет (450-442)/442∙100%=1,8 % (допускается до 5 %).
Условие контактной прочности соблюдается.
2.7 Проверка зубьев на выносливость по напряжениям изгиба
Допускаемое напряжение на изгиб определяется по формуле
[σF]= ![]() , [п.1, формула 24]
, [п.1, формула 24]
где: σFlimb -предел выносливости соответствующему базовому числу циклов. Для стали 45 улучшенной при твердости НВ ≤ 350 = 1,8 НВ [п.1, таблица 3,9]
[SF] – коэффициент безопасности.
[SF] = [SF]΄ [SF]˝,
где: [SF]΄ - коэффициент, учитывающий нестабильность свойств материала зубчатых
колес. (Для стали 45 улучшенной = 1,75) [ п.1, таблица 3,9 ]
[SF]˝ - коэффициент, учитывающий способ получения заготовки зубчатого
колеса. (Для поковок и штамповок = 1,0)
Следовательно, [SF] = 1,75·1 =1,75
Допускаемое напряжение: для
шестерни [σF1] =![]() МПа
МПа
для колеса [σF2]=![]() МПа
МПа
Проверочный расчёт на изгибную прочность проводится по формуле:
![]() [п.1, формула 25],
[п.1, формула 25],
где: YF – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев.
у шестерни ![]() , у колеса
, у колеса ![]() .
.
При этом ![]() 3,9
и
3,9
и ![]() 3,60 [п.1, стр.42]
3,60 [п.1, стр.42]
Yβ –коэффициент, компенсирующий погрешности, возникающие из-за применения той же расчетной схемы зуба, что и в случае прямых зубьев.
KF – коэффициент нагрузки.
КFα – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями. (При 8-й степени точности = 0,91 ) [п.2, стр. 66.]
KF = KFβ KFυ, где: KFβ - коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба. Зависит от ψbd и HB. (При НВ≤ 350 и ψbd =1,07 KFβ =1,11 ) [п.1, табл. 3,7.]
KFυ – коэффициент динамичности. [п.1, табл. 3,8.]
По таблице 3.8[1] при 8-й степени точности и скорости v=1,5
м/с ![]() =1,1.
=1,1.
![]()
Расчёт на изгиб производится для шестерни или колеса в зависимости от отношения
![]() :
:
для шестерни ![]()
для колеса ![]()
Так как для колеса это отношение меньше, расчёт проведём по колесу.
![]()
![]()
![]()
Таким образом, условие прочности на изгиб соблюдается.
|
3. Конструирование и предварительный расчет валов редуктора
Простые по конструкции гладкие валы выполняются одинакового номинального диаметра по всей длине; для обеспечения требуемых посадок деталей предусматриваются на участках вала соответствующие отклонения диаметра. Для удобства сборки и разборки узла вала, замены подшипников и других насаживаемых деталей вала – валы выполняются ступенчатыми. Предварительный расчет проводим на кручение по пониженным допускаемым напряжениям. 3.1. Ведущий вал Материал ведущего вала выбираем такой же, как уже выбранный материал шестерни, предполагая , что шестерню будем выполнять заодно с валом. Диаметр выходного конца вала определяем из расчёта только на кручение по пониженным напряжениям по формуле где: Т1 – крутящий момент ведущего вала, Н мм; [τк] - допускаемое напряжение на кручение, МПа. |
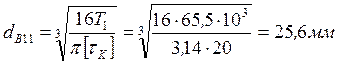
|
Корректируем dв11 по предполагаемому ряду чисел [п.1, стр.161], при необходимости по стандартным размерам муфт (п.1, стр. 268-288). Для двигателя dдв=38 мм, принимаем dв11 =32 мм. Разрабатываем конструкцию вала. Длина ступени l11 под полумуфту l11= (1,0 ÷1,5) dв11=(1,0 ÷1,5) 32=32…48 мм Диаметр второй ступени d2под подшипники качения определяется |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.