|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
|
|
- |
есть |
- |
нет |
- |
- |
да |
- |
много |
1.1 |
|
- |
нет |
- |
есть |
- |
- |
нет |
- |
много |
1.2 |
|
много |
нет |
- |
да |
да |
много |
- |
выше ср |
много |
2.1 |
|
много |
есть |
- |
да |
да |
много |
- |
средняя |
много |
2.2 |
|
мало |
нет |
да |
да |
да |
средне |
- |
высокая |
мало |
2.3 |
|
мало |
- |
- |
да |
да |
мало |
да |
высокая |
мало |
3.1 |
|
много |
- |
- |
да |
да |
много |
да |
средняя |
средне |
3.2 |
|
много |
- |
- |
да |
да |
много |
да |
ниже ср |
много |
3.3 |
|
много |
есть |
да |
- |
да |
много |
нет |
средняя |
много |
4.1 |
|
мало |
нет |
- |
- |
да |
мало |
да |
низкая |
много |
4.2 |
|
мало |
нет |
- |
- |
нет |
много |
да |
средняя |
много |
4.3 |
Априорная информация по условиям протекания ПрС/С «Выход на курс атаки»
1. Координаты цели;
2. Курс выхода на цель;
3. Дальность выхода на курс атаки;
4. Координаты цели;
5. Курс захода на цель;
6. Ограничения по времени выхода;
7. Ограничение по перегрузке;
8. Ограничение по углу крена.
Рассмотрим ситуацию выхода самолета на курс атаки, когда его траектория не пересекает зону угроз.
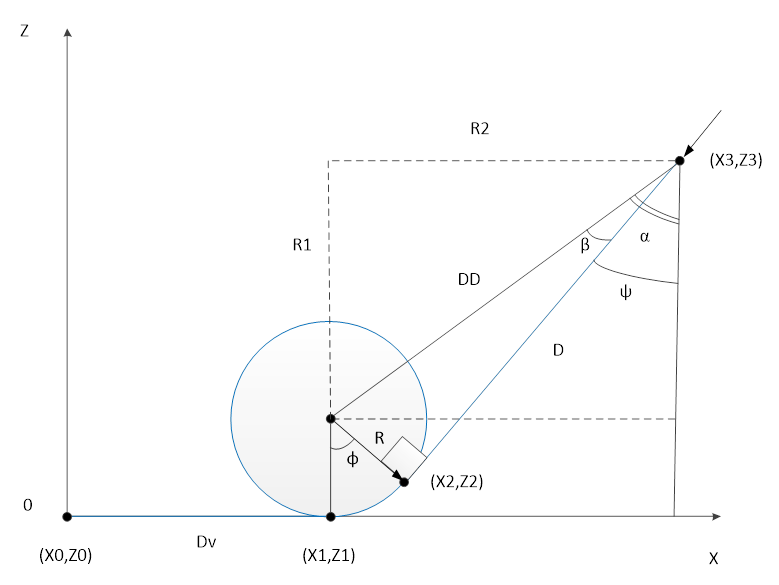
Цель находится в точке (Х0,Z0), самолет – в точке (Х3,Z3).
Траектория движения самолета состоит из:
- прямолинейного участка от (Х3,Z3) до (Х2,Z2);
- разворота по дуге окружности радиуса R (минимальный радиус разворота) от (Х2,Z2) до (Х1,Z1);
- захода на цель.
Найдем координаты точек траектории:
1) Найдем угол ψ:
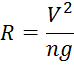
![]()
![]()
![]()
![]()
![]()
![]()
2) Найдем координаты точки (Х2,Z2):
![]()
![]()
![]()
3) Найдем координаты точки (Х1,Z1):
![]()
![]()
![]()
4) Заход на цель (Х0,Z0).
Рассмотренный вариант захода на цель применим для ситуации, когда текущий курс самолета совпадает с необходимым углом ψ. Однако в реальной боевой ситуации курс самолета может быть другим. Поэтому рассчитаем траекторию движения самолета при выходе на необходимый угол ψ.
Задача сводится к добавлению элемента в виде дуги окружности. Это позволяет выделить участок траектории, на котором самолет совершит разворот на необходимый курс.
Для удобства введем систему координат (X’,Z’), начало которой находится в точке (Х3,Z3). Нам известны координаты самолета (Х5,Z5), его курс θ’.
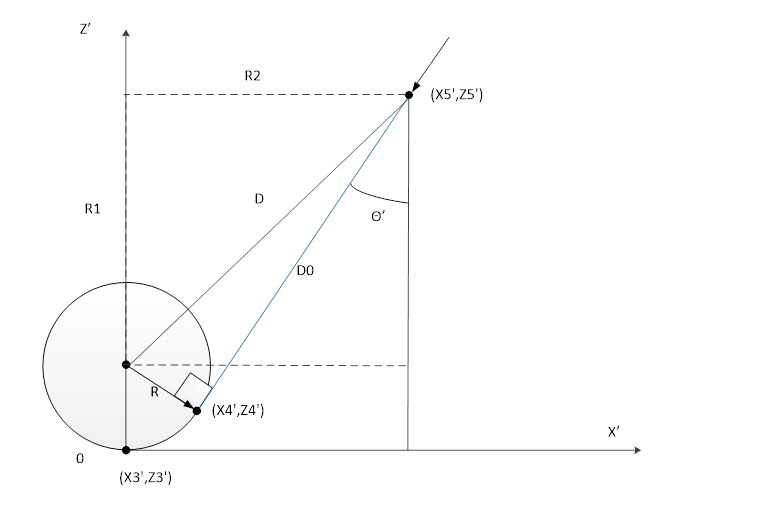
Траектория движения самолета состоит из:
- прямолинейного участка от (Х’5,Z’5) до (Х’4,Z’4);
- разворота по дуге окружности радиуса R (минимальный радиус разворота) от (Х’4,Z’4) до (Х’3,Z’3);
Найдем координаты точек траектории:
1) Найдем D0
![]()
![]()
![]()
2) Найдем координаты точки (Х’4,Z’4):
![]()
![]()
![]()
3) Найдем координаты точки (Х’3,Z’3):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.