Системное проектирование авиационных боевых комплексов, страница 10

Решение данной задачи позволяет полностью охватить все возможные курсы полета самолета и его начальные положения путем изменения исходных данных.

БЦВМ-алгоритм конструирования траектории выхода на предпочтительный курс атаки (веер курсов)

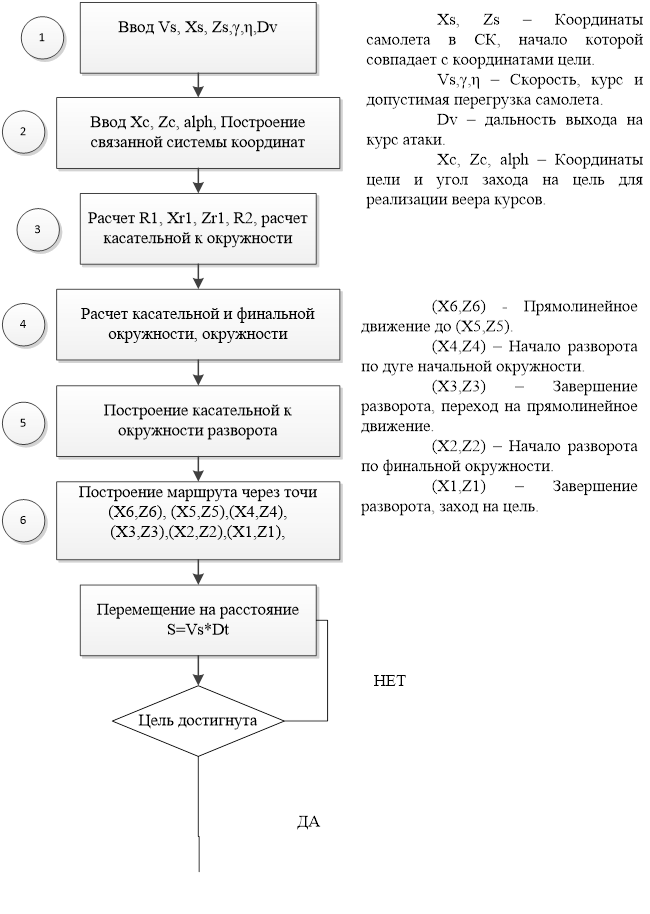
Расчеты были произведены в программе, написанной на языке С/С++ в среде разработки VisualStudio 2010;

Представим код программы для каждого блока алгоритма:

1:

Vs = 250;

Xs = 20000;

Zs = 15000;

n = 2.5;

gamma = 30*Pi/180;

Dv = 5000;

2:       //Вводим координаты цели и угол захода на нее

doubleXc = 15000;

doubleZc = 15000;

doublealph = 30;

//Строим систему координат, начало которой совпадает с положением цели, а угол захода с осью X

void DrawSK2 (double x0, double z0, double angle)

{

while (angle >= 2*Pi) angle -= 2*Pi;

doubleNew_Top_Z, New_Down_Z;

doubleNew_Left_X, New_Right_X;

x0 = MashtabX(x0);

z0 = MashtabZ(z0);

New_Top_Z = z0+tan(angle)*(Left_X-x0);

New_Down_Z = z0+tan(angle)*(Right_X-x0);

New_Left_X = x0+tan(angle)*(z0-Down_Z);

New_Right_X = x0+tan(angle)*(z0-Top_Z);       

SelectObject(hdc, Brush_bl);

Ellipse (hdc, x0-4, z0-4, x0+4, z0+4);

if (angle == 90*Pi/180)

{

MoveToEx(hdc, x0 ,Top_Z, NULL );

LineTo(hdc, x0, Down_Z);

MoveToEx(hdc, Left_X ,z0, NULL );

LineTo(hdc, Right_X, z0);

}

elseif (angle == 270*Pi/180)

{

MoveToEx(hdc, x0 ,Down_Z, NULL );

LineTo(hdc, x0, Top_Z);

MoveToEx(hdc, Right_X ,z0, NULL );

LineTo(hdc, Left_X, z0);

}     

else

{

MoveToEx(hdc, Left_X , New_Top_Z, NULL );

LineTo(hdc, Right_X, New_Down_Z );

MoveToEx(hdc,  New_Left_X ,Down_Z, NULL );

LineTo(hdc, New_Right_X , Top_Z);

}

3:

//минимальный радиус разворота

R =  Vs*Vs / (g*n);

// расчет положения начальной окружность разворота          

R1=    R;                                           

Xr1= Xs - R1*sin(gamma);

Zr1= Zs - R1*cos(gamma);  

// расчет положения финальной окружность разворота                

R2=    R;                                           

Xr2= Dv;

Zr2= R2;

4:

// функция находит точки касания к двум окружностям

void Tangent (double Xr1, double Zr1, double R1, double Xr2, double Zr2,double R2, double *Xk1, double *Zk1, double *Xk2, double*Zk2, double *angle)

{

double alpha1 = asin ( (R1-R2)/ sqrt ( (Zr2-Zr1)*(Zr2-Zr1)+(Xr2-Xr1)*(Xr2-Xr1) ) );

double alpha2 = atan ( (Zr2-Zr1)/(Xr2-Xr1) );

double alpha = alpha1 + alpha2;

*Xk1 = Xr1 + R1 * sin (alpha);

*Zk1 = Zr1 - R1 * cos (alpha);

*Xk2 = Xr2 + R2 * sin (alpha);

*Zk2 = Zr2 - R2 * cos (alpha);

*angle = atan( (*Zk2-*Zk1) / (*Xk2-*Xk1) );

}

// поиск точек (Х2,Z2) и (Х3,Z3);

Tangent (Xr1, Zr1, R1, Xr2, Zr2, R2, &Xk1, &Zk1, &Xk2, &Zk2,&angle);

5,6,7:

//поиск точек (Х2,Z2) и (Х3,Z3);

Tangent (Xr2, Zr2, R2, Xzu, Zzu, Rzu, &Xk1, &Zk1, &Xk2, &Zk2,&angle);

// Точка пересечения касательной и линии траектории движения самолета

CrossPoint (Xk1, Zk1, Xk2, Zk2, Xs,Zs,Xs+3000*cos(gamma),Zs-3000*sin(gamma),&Xcr,&Zcr);

//поиск точек (Х4,Z4) и (Х5,Z5);

psi = angle;

Xr1= Xcr - R1 * sin( Pi/2 + gamma/2 - psi/2 ) / sin( psi/2 + gamma/2 );

Zr1= Zcr - R1 * cos( Pi/2 + gamma/2 - psi/2 ) / sin( psi/2 + gamma/2 );

X4 = Xcr - R * sin (Pi/2 - psi) / tan ( psi/2 + gamma/2 );

Z4 = Zcr - R * cos (Pi/2 - psi) / tan ( psi/2 + gamma/2 );

X5 = Xcr - R * cos (gamma) / tan ( psi/2 + gamma/2 );

Z5 = Zcr + R * sin (gamma) / tan ( psi/2 + gamma/2 );

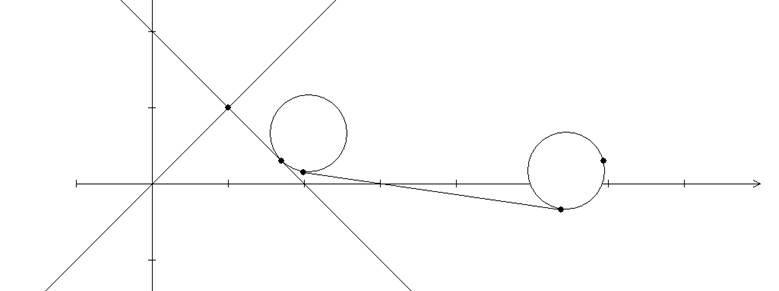
Результат работы программы для случаев, когда координаты цели и угол захода на нее не совпадают с «нулевыми» (вводи связанную систему координат):

1) 

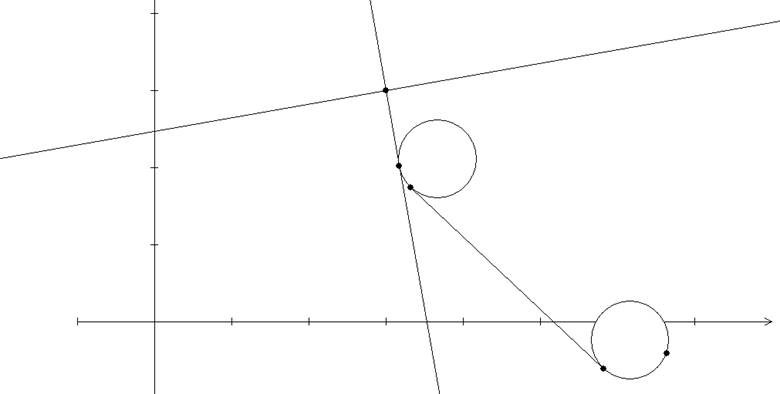
2) 

3) 

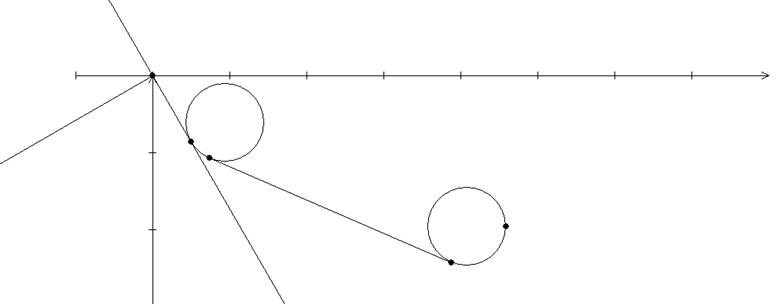
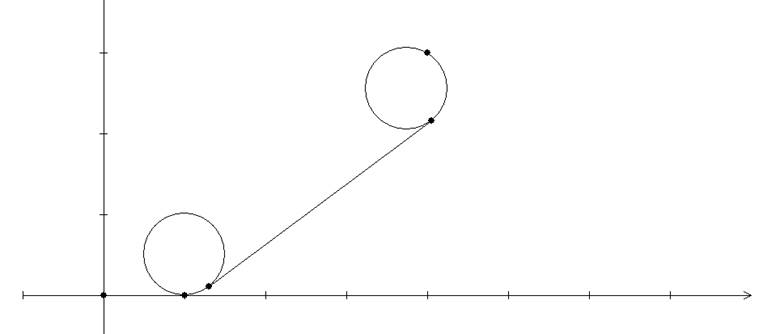
Результат работы программы для случаев, когда координаты цели и угол захода на нее совпадают с «нулевыми» (связанная система координат не вводится):