Метод парабол для решения нелинейных уравнений

СОДЕРЖАНИЕ

ТЖК. 0. ПК-1-11.02. КР.

Лист

2

Изм.

Лист.

N докум.

Подп.

Дата

ВВЕДЕНИЕ

Задача нахождения точного значения определенного интеграла не всегда имеет решение. Действительно, первообразную подынтегральной функции во многих случаях не удается представить в виде элементарной функции. В этом случае мы не можем точно вычислить определенный интеграл по формуле Ньютона-Лейбница. Однако есть методы численного интегрирования, позволяющие получить значение определенного интеграла с требуемой степенью точности. Одним из таких методов является метод Симпсона (его еще называют методом парабол).

Сначала выясним смысл метода парабол, дадим графическую иллюстрацию и выведем формулу для вычисления приближенного значения интеграла. Следом перейдем к решению характерных примеров, снабдим их подробными комментариями.

ВВЕДЕНИЕ

Лист

3

Изм.

Лист.

N докум.

Подп.

Дата

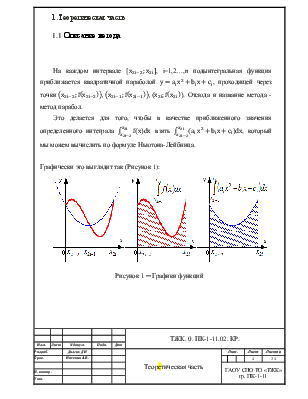
1.Теоретическая часть

1.1 Описание метода

На каждом интервале , i=1,2…,n подынтегральная функция приближается квадратичной параболой , проходящей через точки. Отсюда и название метода - метод парабол.

Это делается для того, чтобы в качестве приближенного значения определенного интеграла  взять , который мы можем вычислить по формуле Ньютона-Лейбница.

Графически это выглядит так (Рисунок 1):

Рисунок 1 ─ Графики функций

ТЖК. 0. ПК-1-11.02. КР.

Изм.

Лист

N докум.

Подп.

Дата

Разраб.

Д.Н

Теоретическая часть

Лит.

Лист

Листов

Пров.

А.В.

4

24

ГАОУ СПО ТО «ТЖК»

гр. ПК-1-11

Н. контр.

Утв.

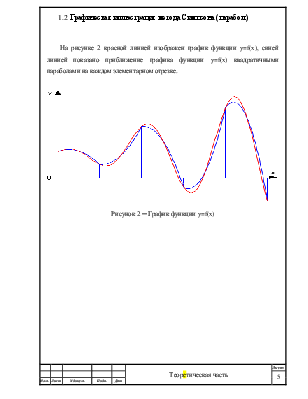
1.2 Графическая иллюстрация метода Симпсона (парабол)

На рисунке 2 красной линией изображен график функции y=f(x), синей линией показано приближение графика функции y=f(x) квадратичными параболами на каждом элементарном отрезке.

Рисунок 2 ─ График функции y=f(x)

Теоретическая часть

Лист

5

Изм.

Лист.

N докум.

Подп.

Дата

1.3 Вывод формулы метода Симпсона (парабол)

В силу пятого свойства определенного интеграла имеем:

Для получения формулы метода парабол (Симпсона) нам осталось вычислить:

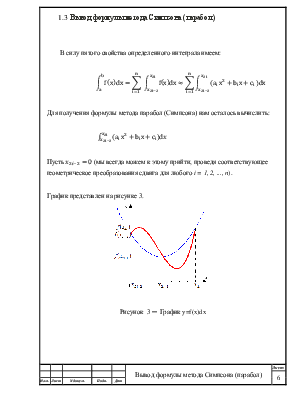
Пусть  (мы всегда можем к этому прийти, проведя соответствующее геометрическое преобразования сдвига для любого i = 1, 2, ..., n).

График представлен на рисунке 3.

Рисунок  3 ─  График y=f(x)dx

Вывод формулы метода Симпсона (парабол)

Лист

6

Изм.

Лист.

N докум.

Подп.

Дата

Продемонстрируем, что через точки

 проходит только одна квадратичная парабола . Другими словами, докажем, что коэффициенты  определяются единственным образом.

Так как   - точки параболы, то справедливо каждое из уравнений системы:

Записанная система уравнений есть система линейных алгебраических  уравнений относительно неизвестных переменных . Определителем основной матрицы этой системы уравнений является определитель Вандермонда  , а он отличен от нуля для несовпадающих точек  . Это указывает на то, что система уравнений имеет единственное решение (об этом говорится в статье решение систем линейных алгебраических уравнений), то есть, коэффициенты  определяются единственным образом, и через точки проходит единственная квадратичная парабола.

Перейдем к нахождению интеграла:  

Из этого следует:

Вывод формулы метода Симпсона (парабол)

Лист

7

Изм.

Лист.

N докум.

Подп.

Дата

Используем эти равенства, чтобы осуществить последний переход в следующей цепочке равенств:

Таким образом, можно получить формулу метода парабол:

Формула метода Симпсона (парабол) имеет вид:

Вывод формулы метода Симпсона (парабол)

Лист

8

Изм.

Лист

N докум.

Подп.

Дата

1.4. Пример приближенного вычисления методом Симпсона (парабол)

Пример.

Вычислите определенный интеграл  методом Симпсона, разбив отрезок интегрирования на 5 частей.

Решение.

Из условия мы знаем, что a = 0; b = 5; n = 5;  

Формула метода Симпсона (парабол) имеет вид

Для ее применения нам требуется вычислить шаг  , определить узлы  и вычислить соответствующие значения подынтегральной функции .

Промежуточные вычисления будем проводить с точностью до четырех знаков (округлять на пятом знаке).

Итак, вычисляем шаг  .

Переходим к узлам и значениям функции в них:

Пример приближенного вычисления методом Симпсона (парабол)

Лист

9

Изм.

Лист.

N докум.

Подп.

Дата

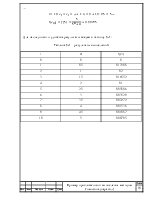
Для наглядности и удобства результаты сведем в таблицу №1:

Таблица №1 – результаты вычислений:

Пример приближенного вычисления методом Симпсона (парабол)

Лист

10

Изм.

Лист

N докум.

Подп.

Дата

Подставляем полученные результаты в формулу метода парабол:

Мы специально взяли определенный интеграл, который можно вычислить по формуле Ньютона-Лейбница, чтобы сравнить результаты.

Результаты совпадают с точностью до сотых.

Пример приближенного вычисления методом Симпсона (парабол)

Лист

11

Изм.

Лист.

N докум.

Подп.

Дата

2. Практическая часть

2.1. Блок-схема программы

На рисунке 4 представлена блок-схема программы

Рисунок 4 ─ Блок-схема метода Симпсона

ТЖК. 0. ПК-1-11.02. КР.

Изм.

Лист

N докум.

Подп.

Дата

Разраб.

Практическая часть

Лит.

Лист

Листов

Пров.

12

24

ПК-1-11

Н. контр.

Утв.

2.2. Разработка интерфейса

Графический интерфейс представляет собой стандартный набор