Симплекс-метод в решении задач линейного программирования
Теоретические сведения
Пример решения задачи ЛП Симплекс-методом
Графический метод в решении задач линейного программирования
Теоретические сведения
Графический метод основан на геометрической интерпретации задачи ЛП и применяется в основном при решении задач в двумерном пространстве.
![]()
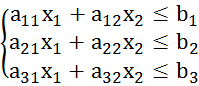
![]()
![]()
Необходимо найти вектор ![]() ,
который удовлетворяет системе ограничений и минимизирует функцию Z.
,
который удовлетворяет системе ограничений и минимизирует функцию Z.
Каждое неравенство ![]() определяет
в плоскости Х10Х2 полуплоскость с граничной прямой
определяет
в плоскости Х10Х2 полуплоскость с граничной прямой ![]() .
Точки, лежащие в полуплоскости, удовлетворяют данному неравенству.
.
Точки, лежащие в полуплоскости, удовлетворяют данному неравенству.
Тривиальные неравенства определяют первый квадрат в системе координат.
Множество точек пересечения всех этих полуплоскостей образуют многоугольник решений (область допустимых решений ОДР).
Каждая точка этого многоугольника есть решение системы ограничений (допустимый план задачи ЛП).
Многоугольник решений может быть и неограничен областью или выражаться в прямую, луч, отрезок или вообще в точку.
Если ОДР пустая, то система ограничений несовместна.
Графическое решение задачи ЛП начинают с построения многоугольника решений.
При фиксированном Z=Z0
равенство![]() представляет
собой уравнение прямой, называемой линией уровня, для всех точек которой
функция принимает одно и тоже значение
представляет
собой уравнение прямой, называемой линией уровня, для всех точек которой
функция принимает одно и тоже значение ![]() .
.
Если перемещать эту прямую в направлении вектора
![]() это выражение называется антиградиентом, которое показывает направление
убывания функции.
это выражение называется антиградиентом, которое показывает направление
убывания функции.
Антиградиент всегда должен быть перпендикулярен линии уровня.
Далее будем перемещать линию уровня до тех пор, пока она не окажется в таком положении, что все точки многоугольника решений будут лежать по одну её сторону, или хотя бы одна точка будет лежать на этой прямой.
Таких положений может быть не более двух. Одно из них соответственно min, а другое max.
Соответствующая точка ![]() называется
оптимальным планом и является решением задачи ЛП.
называется
оптимальным планом и является решением задачи ЛП.
Если же ОДР не замкнута, то одно или оба этих положений могут отсутствовать.
Очевидно, что прямая ![]() проходит хотя бы через одну условную точку многоугольника решений, поэтому
оптимальному плану соответствует хотя бы одна условная точка.
проходит хотя бы через одну условную точку многоугольника решений, поэтому
оптимальному плану соответствует хотя бы одна условная точка.
Линия уровня может совпадать со стороной многоугольника решений, в этом случае оптимальное решение не единственно (альтернативный оптимум) – оптимальными планами являются обе условные точки и все точки отрезка между ними (∞). Значение функции во всех точках альтернативного оптимума будет одно и тоже.
1. Допустимая область всегда является выпуклым множеством, даже в том случае, когда она ограничена.
2. Оптимальное решение всегда достигается в вершине допустимой области.
3. Если оптимальное решение не одно, то значение функции совпадает во всех точках решения.
Пример решения задачи ЛП графическим методом
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
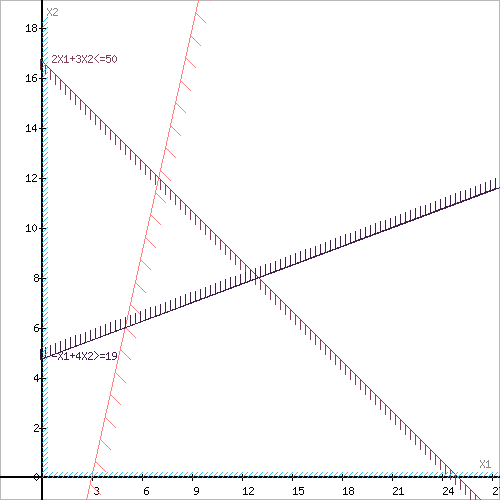
или
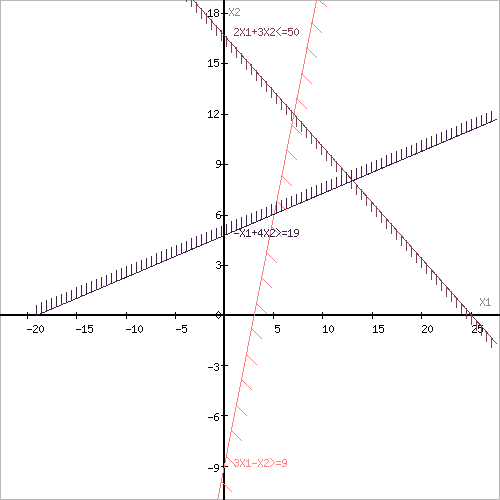
Границы области допустимых решений
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений.
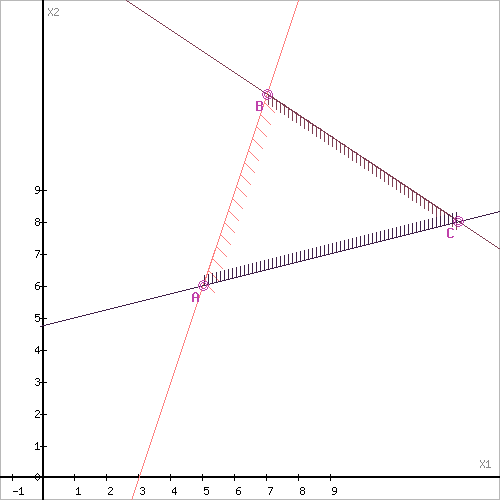
Рассмотрим целевую функцию задачи F = x1+5x2 → min. Построим прямую, отвечающую значению функции F = 0: F = x1+5x2 = 0. Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
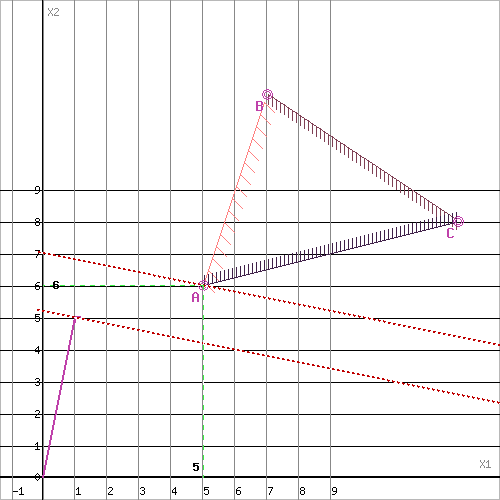
Равный масштаб

Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых(1) и (3), то ее координаты удовлетворяют уравнениям этих прямых: 3x1-x2≥9 -x1+4x2≥19 Решив систему уравнений, получим: x1 = 5, x2 = 6 Откуда найдем минимальное значение целевой функции: F(X) = 1*5 + 5*6 = 35
Симплекс-метод в решении
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.