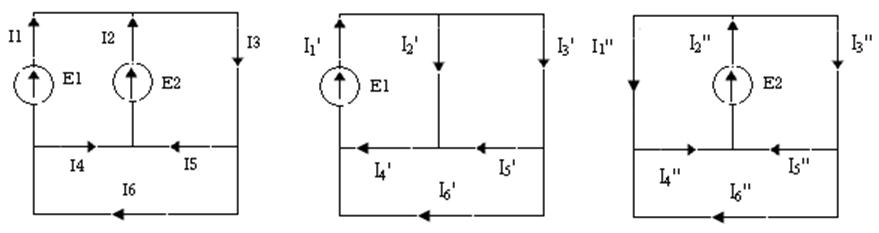
Электротехника \ Теоретические основы электротехники

Изучение и экспериментальная проверка основных свойств линейных электрических цепей постоянного тока, страница 2

1 2 3

5. Проверяем выполнение первого закона Кирхгоффа для всех узлов остовов схем 1, 2, 3. Проверку можно считать удовлетворительной, если левая и правая части уравнений отличаются друг от друга на величину, не большую суммы абсолютных погрешностей отдельных измерений. Измерение токов проводится одинаковыми миллиамперметрами, поэтому для любого узла должно выполняться условие:

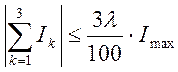где γ = 1,5 – класс точности прибора;

I_max = 1мА – верхний предел измерения прибора.

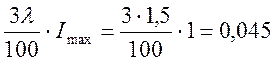
Проверка первого закона для Е₁ + Е₂:

I₂+ I₁– I₃=0; 0,29 + 0,42 -0,72 = -0,01;

I₄+ I₅– I₂=0; 0,06 + 0,23 - 0,29 = 0;

I₆– I₁– I₄=0; 0,46 – 0,42 – 0,06 = -0,02;

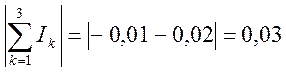
0,03 ≤ 0,045

Из этого следует, что для двух источников ЭДС Е₁ + Е₂ первый закон Кирхгоффа выполняется.

I₁– I₂– I₃=0; 0,62 – 0,2 – 0,45 = -0,03;

I₅– I₄+ I₂=0; 0,07 – 0,25 + 0,2 = 0,02;

I₄– I₁+ I₆=0. 0,25 – 0,07 – 0,37 = 0.

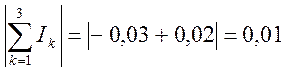
0,01 ≤ 0,045

Из этого следует, что для источника ЭДС Е₁ первый закон Кирхгоффа выполняется.

Проверка первого закона для Е₂:

I₂– I₁– I₃=0; 0,47 -0,2 – 0,27 = 0;

I₄+ I₅- I₂=0; 0,29 + 0,16 – 0,47 = -0,02;

I₁– I₄+ I₆=0. 0,2 – 0,29 + 0,09 = 0.

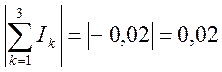
0,02 ≤ 0,045

Из этого следует, что для источника ЭДС Е₂ первый закон Кирхгоффа выполняется.

6. Проверяем выполнение принципа наложения для токов: ток в любой ветви схемы равен алгебраической сумме частичных токов от действия каждого источника в отдельности.

I₁= I₁^'– I₁^''; I₁= 0,42;

I₂= I₂^'– I₂^''; I₂= 0,27;

I₃= I₃^'– I₃^''; I₃= 0,72;

I₄= I₄^'– I₄^''; I₄= 0,04;

I₅= I₅^'– I₅^''; I₅= 0,23;

I₆= I₆^'– I₆^''. I₆= 0,43.

Сравниваем результаты измерения токов от действия сразу двух источников и токов I^∑, полученных в результате алгебраического суммирования частичных токов от каждого источника в отдельности. Принцип наложения выполняется, если

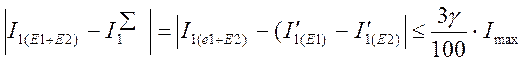где γ = 1,5 – класс точности прибора;

I_max = 1мА – верхний предел измерения миллиамперметра.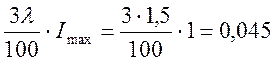

0,42 – 0,42 = 0 ≤ 0,045 – неравенство выполняется;

0,29 – 0,27 = 0,02 ≤ 0,045 – неравенство выполняется;

0,72 – 0,72 = 0 ≤ 0,045 – неравенство выполняется;

0,06 – 0,04 = 0,02 ≤ 0,045 – неравенство выполняется;

0,23 – 0,23 = 0 ≤ 0,045 – неравенство выполняется;

0,46 – 0,43 = 0,03 ≤ 0,045 – неравенство выполняется.

Из этих выражений следует, что принцип наложения для токов выполняется.

Задание 3.

Линейные соотношения в электрических цепях.

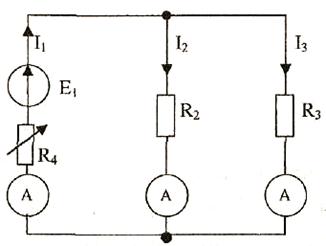
1. Собираем схему установки.

2. Устанавливаем переменный резистор R₄ в положение, соответствующее минимальному значению величины сопротивления, и измеряем токи в ветвях. Результаты записываем в таблицу.

3. Устанавливаем переменный резистор R₄ в положение, соответствующее максимальному значению величины сопротивления, и измеряем токи в ветвях. Результаты записываем в таблицу.

4. Устанавливаем переменный резистор R₄ в положение, соответствующее среднему значению величины сопротивления, и измеряем токи в ветвях. Результаты записываем в таблицу.

Значение переменного значения R₄	I₁, mA	I₂, mA	I₃, mA
R₄min	1	0,2	0,8
R₄max	0,35	0,07	0,28
R₄сред	0,62	0,12	0,5

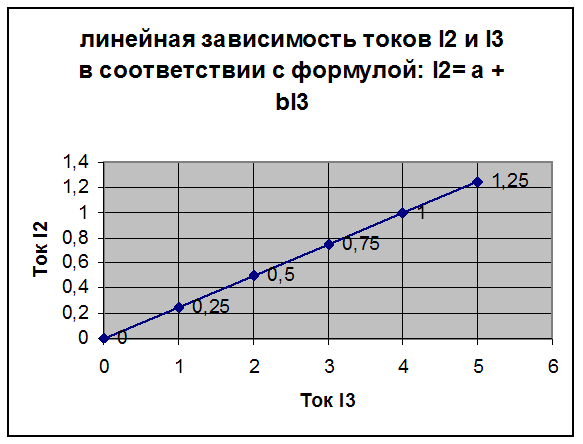
5. Составляем уравнение, связывающее линейной зависимостью токи I₂и I₃ в соответствии с формулой:

I_k= a + bI_m

Определяем коэффициенты этого уравнения a и b.

I₂= a + bI₃

I₂⁽¹⁾= a + bI₃⁽¹⁾

I₂⁽²⁾= a + bI₃⁽²⁾

Где I₂⁽¹⁾ и I₃⁽¹⁾- токи первого опыта;

I₂⁽²⁾ и I₃⁽²⁾- токи второго опыта.

Подставляем значения и решаем систему уравнений, находим коэффициенты a и b.

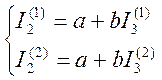
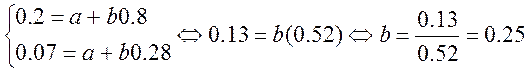
a= 0,2- 0,25·0,8= 0

Проверка:

Подставим в уравнение I₂= a + bI₃ рассчитанные значение a и b и ток I₃ из таблицы.

I₂= 0+0,25·0,5=0,125; 0,125 ≈ 0,12.

Построим график линейной зависимости токов:

Задание 4.

Входные и взаимные проводимости ветвей. Изучение принципа взаимности.

1. Для проведения опыта используется схема:

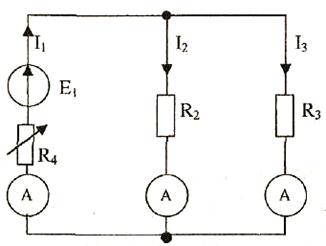ЭДС Е₁ включена в первую ветвь. Устанавливаем переменный резистор R₄ в положение, соответствующее среднему значению величины сопротивления. Замеряем токи в ветвях I_1,I_2, I₃. Результаты записываем в таблицу.

2. Включаем источник ЭДС во вторую ветвь. Замеряем токи в ветвях I_1,I_2, I₃. Результаты записываем в таблицу.

3. . Включаем источник ЭДС в третью ветвь. Замеряем токи в ветвях I_1,I_2, I₃. Результаты записываем в таблицу.

Номер ветви, в которую включена ЭДС	Токи ветвей, mA
Номер ветви, в которую включена ЭДС	I₁	I₂	I₃
Первая	0,62	0,12	0,5
Вторая	0,15	0,62	0,47
Третья	0,5	0,48	0,98

4. Замеряем величину ЭДС Е₁.

Е₁= 11,4 В.

5. Формируем матрицу входных и взаимных проводимостей ветвей, используя формулы:

Отношение тока К – ой ветви I_k к ЭДС Е_к которая также включена в К – ю ветвь, называется входной проводимостью ветви:

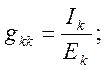
Отношение тока М – ой ветви I_М к ЭДС Е_к которая также включена в К – ю ветвь, называется взаимной проводимостью между ветвями К и М:

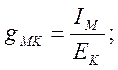
В результате формируется матрица :

;

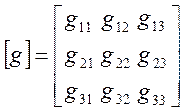Для любой линейной электрической цепи выполняется условие:

g_KM = g_MK,

где g_KM , g_MK – взаимные проводимости между ветвями М и К.

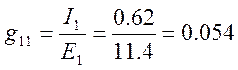
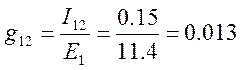
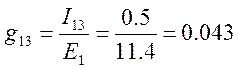
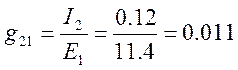
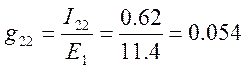
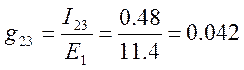
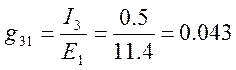
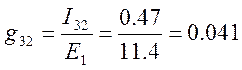
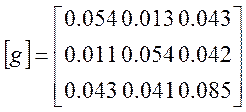
Члены матрицы симметричны относительно главной оси. Токи активных ветвей различны, а токи взаимнопассивных ветвей одинаковы.

Задание 5.

Исследование теоремы об эквивалентном генераторе.

1. Для проведения опыта используется схема:

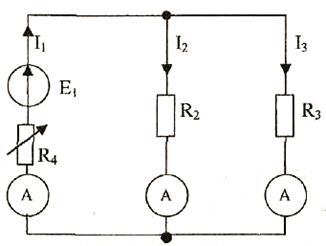ЭДС Е₁ включена в первую ветвь. Устанавливаем переменный резистор R₄ в положение, соответствующее среднему значению величины сопротивления.

Определяем ток методом эквивалентного генератора в ветви 3.

2. Определяем сопротивление резистора заданной ветви 3 методом амперметра и вольтметра. Для этого измеряем на резисторе заданной ветви напряжение U₃ и ток I₃, протекающий через резистор.

I₃ = 0,5 мА;

U₃ = 1,6 В.

Тогда

R₃ =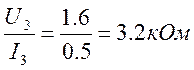

3. Определяем напряжение холостого хода U_хх. Для этого исключаем из схемы резистор R₃ и на оставшихся зажимах измеряем напряжение U_хх.

U_хх = 5,8 В.

4. Определяем ток короткого замыкания I_кз. Для этого зашунтируем резистор R₃ перемычкой (короткое замыкание) и замерим ток, протекающий в ветви.

I_кз = 0,7 мА

5. Аналитически определяем входное сопротивление.

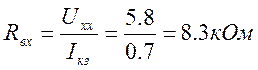
6. Рассчитываем ток в ветви 3 методом эквивалентного генератора.

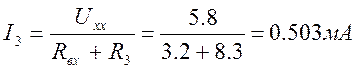
7. Сравним рассчитанное значение тока I₃ с током, измеренным в пункте 2 текущего задания:

0,5 ≈ 0,503

Применив теорему об эквивалентном генераторе, и рассчитав значение параметров, мы показали, что значение, рассчитанное теоретически равно значению полученному экспериментально.

1 2

Скачать файл