





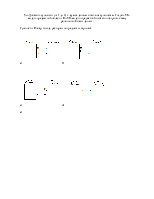



№1.1. Выяснить взаимное расположение множеств D, E, F, если A, B, C –произвольные подмножества U. Указать расположение множеств на карте Карно. Записать минимальные нормальные формы для искомых множеств.
D: (A⋂ C)⋂ (B\C)∪ ¬(A∪ B)
E: (A⋂ C)∪ ¬(B∪ C)
F: C∪ ¬A∪ B
D: A˄C˄(B˄¬C)˅(¬A˄¬B) ⇔ ¬A˄¬B ДНФ(D) = ¬A˄¬B КНФ(D) = ¬A˄¬B
|
A/BC |
00 |
01 |
11 |
10 |
|
0 |
+ |
+ |
||
|
1 |
E: (A˄C)˅(¬B˄¬C) ДНФ(E) = (A˄C)˅(¬B˄¬C)
КНФ(E) = (A˅¬C)˄(¬B˅C)
|
A/BC |
00 |
01 |
11 |
10 |
|
0 |
+ |
|||
|
1 |
+ |
+ |
+ |
F: C˅¬A˅B ДНФ(F) = C˅¬A˅B КНФ(F) = C˅¬A˅B
|
A/BC |
00 |
01 |
11 |
10 |
|
0 |
+ |
+ |
+ |
+ |
|
1 |
+ |
+ |
+ |
Ответ: D нормально пересекается с E, D ⊂ F, E нормально пересекается с F
№1.2. Проверить, что для любых множеств A, B, C выполнение включения α влечет выполнение включения β. Проверить другие возможные импликации.
α: A∪ B ⊆ C
β: (B\C)∪ (A\B) ⊆ A ⋂ C
α: (a˅b) ⇒ c
β: ((b˄¬c)˅(a˄¬b)) ⇒ (a˄c) α ⇔ β ≡ 1 ⇒ включения α влечет выполнение включения β
α1: c ⇒ (a˅b)
β1: (a˄c) ⇒ ((b˄¬c)˅(a˄¬b))
|
a |
b |
c |
α |
β |
α1 |
β1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
№1.3. Для произвольных множеств A, B, H проверить, является ли выполнение включения α необходимым и достаточным условием выполнения равенства β. Проверить другие возможные импликации.
α: A ∪ B ⊆ H
β: A⋂B = ((AΔB)\H)∪(A⋂B⋂H)
α: (a˅b) ⇒ h
β: (a˄b) ⇔ (((a⊕b)˄¬h)˅(a˄b˄h))
α1: h ⇒ (a˅b)
|
a |
b |
h |
α |
β |
α1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
β ⇒ α ≡ 1 ⇒ включение α является необходимым и достаточным условием выполнения равенства β
№1.4. Выяснить, верно ли равенство α для произвольных A, B, C.
α: C x (A\B) = (C x B)\(C x (A∪ B))
C x (A\B) = C x (B \ (A∪ B))
c x (b ˄ ¬(a˅b)) = c x (b˄¬a˄¬b) = 0
C x (A\B) = 0 – верно не для всех A B C
№2. На любом языке процедурного программирования записать алгоритм нахождения для заданного множества:
- Всех подмножеств
- Всех подмножеств с заданным количеством элементов
- Всех разбиений множества
- Всех перестановок множества
//Вывод подмножества без учета размера. Шестернин ИВБ-4-12
#include <iostream>
using std::cin;
using std::cout;
int main()
{
//Ввод размера множества
int f;
cin >> f;
//Запись множества в массив
int *A = new int[f];
for(int k=0;k<f;k++)
cin >> A[k];
//Создание кода Грея
short *B = new short[f];
for(int k=0;k<f;k++)
B[k]=0;
//Генерация всех подмножеств
int i=0,p,j;
do
{
for(int k=0;k<f;k++)
{
if(B[k]==1)
cout << A[k] << ' ';
}
cout << '\n';
//Создание следующего кода Грея
i++;
p=0;
j=i;
while (j%2==0)
{
j=j/2;
p++;
}
if(p<f)
B[p]=1-B[p];
}
while (p<f);
delete[] B;
delete[] A;
return 0;
}
//Вывод подмножества с учетом размера. Шестернин ИВБ-4-12
#include <iostream>
using std::cin;
using std::cout;
int main()
{
//Ввод размера множества
int f;
cin >> f;
//Ввод предела размера подмножества
int length;
cin >> length;
//Запись множества в массив
int *A = new int[f];
for(int k=0;k<f;k++)
cin >> A[k];
//Создание кода Грея
short *B = new short[f];
for(int k=0;k<f;k++)
B[k]=0;
//Генерация всех подмножеств
int i=0,p,j,amount;
do
{
//Подсчет количества элементов в подмножестве
amount=0;
for(int k=0;k<f;k++)
if(B[k]==1)
amount++;
//Вывод подмножества, если количество его элементов равно size
if(amount==length)
{
for(int k=0;k<f;k++)
{
if(B[k]==1)
cout << A[k] << ' ';
}
cout << '\n';
}
//Генерация следующего кода Грея
i++;
p=0;
j=i;
while (j%2==0)
{
j=j/2;
p++;
}
if(p<f)
B[p]=1-B[p];
}
while (p<f);
delete[] B;
delete[] A;
return 0;
}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.