Економічний зміст вивчення собівартості зернової продукції.Застосування методу аналітичних групувань, страница 2

Показники ряду	Символи	Роки
		2012	2013	2014	2015	2016
Рівень ряду (назва, одиниця виміру)	У	12,5	15,8	14,3	14,5	13,2
Абсолютний приріст: базисний ланцюговий		× ×	3,3 3,3	1,8 -1,5	2 0,2	0,7 -1,3
Коефіцієнт зростання: базисний ланцюговий		× ×	1,264 1,264	1,440 0,905	1,160 1,014	1,056 0,910
Темп зростання: базисний ланцюговий		× ×	126,4 126,4	144 90,5	116 101,4	105,6 91,0
Темп приросту: базисний ланцюговий		× ×	26,4 26,4	44,0 -9,5	16,0 1,4	5,6 -9,0
Абсолютне значення одного процента приросту		×	0,1	0,2	0,1	0,1

Висонок:

Для того, щоб мати узагальнюючі характеристики ряду динаміки 1 ц зернової продукції за 2012-2016 роки, використовуючи аналітичні показники ряду динаміки капіталовкладень із табл. 1, розраховуємо також середні показники: середній рівень динамічного ряду, середні значення з аналітичних показників.

Ми маємо інтервальний ряд з рівними інтервалами часу тому застосуємо середню арифметичну просту.

За даними таблиці виконую розрахунок середніх значень аналітичних показників ряду динаміки за наступними формулами:

1. Середній рівень інтервального ряду визначається за формулою      середньої арифметичної простої з рівнів ряду:   

У =  12,5+15,8+14,3+14,5+13,2  =  70,3 = 14,1 грн

5                  5        

2. Середній абсолютний приріст розраховується за формулою середньої арифметичної простої з ланцюгових приростів:

3. Середній коефіцієнт зростання визначається за формулою середньої геометричною з ланцюгових коефіцієнтів зростання:                     

4. Середній темп зростання дорівнює:  .

5. Середній темп приросту:   .

Висновки

2.2.Виявлення тенденцій собівартості зернової продукції

Таблиця 2

Розрахунок ковзної середньої (трьохрічної)

динаміки показника

Рік	Рівень ряду	Трьохріччя	Рівень ряду		Приріст середнього рівня
			сума за 3 роки	середня за рік
2012	12,5	-	-	-	-
2013	15,8	2012-2014	42,6	14,2	×
2014	14,3	2013-2015	44,6	14,9	0,7
2015	14,5	2014-2016	42,0	14,0	-0,9
2016	13,2	-	-	-	-

Висновок: Зробивши розрахунок ковзної середньої динаміки зернової продукції можу зробити висновок що виявити тенденцію не можемо, через значні коливання рівнів ряду динаміки за 5 років. Доцільно застосовувати прийом аналітичне вирівнювання.

Аналітичне вирівнювання рядів динаміки проводиться за допомогою математичної формули, яка найбільш точно відображає загальну тенденцію ряду.

При вирівнюванні динамічних рядів за допомогою прямої лінії У_t=а₀+а₁t , параметри прямої визначаються за системою рівнянь:

                                               а₀ п + а₁ Σt = Σу

                                               а₀ Σt + а₁ Σt²= Σtу;

Звідки: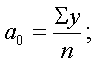                   

     

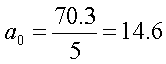
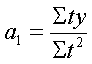
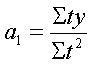
Для проведення допоміжних розрахунків рекомендується використовувати наступний макет таблиці (табл. 3).

Таблиця 3

Вихідні та розрахункові дані

для вирівнювання ряду динаміки за рівнянням прямої

Роки	Порядковий номер року	Фактичний рівень показника	Розрахункові величини			Теоретичний рівень показника
П	t	У	tу		a1t	уt
2012	-2	12,5	-25,0	4	-2,10	11,96
2013	-1	15,8	-15,8	1	-1,05	13,01
2014	0	14,3	0	0	0	14,06
2015	1	14,5	14,5	1	1,05	15,11
2016	2	13,2	26,4	4	2,10	16,16
Разом	х	70,3	0,1	10	х	70,3

Висновок: Застосувавши прийом виявлення загальної тенденції на основі аналітичного вирівнювання за рівнем прямої лінії можна стверджувати, що тенденція собівартості 1 ц зернової продукції за досліджуваний період - зростає. При цьому щорічний приріст складає 1.05 грн.

Для наочного зображення тенденції показників динаміки собівартості 1 ц зернової продукції застосовуємо лінійну діаграму.