Разработка программы на языке С++ на основе структурной методологии., страница 6

На рис. 9.   приведено содержимое стека, соответствующее операциям чтения элементов из g  слева  направо. Целое значение  над I-й конфигурацией стека указывает на то, что в данный момент читается x_i-й символ.

Для реализации стека на  Фортране мы возьмем одномерный  массив  STORE [описанный как  STORE (M)] и  целую переменную с именем ТОР. Всегда, когда нам  нужно поместить на вершину стека элемент Х(I), мы выполняем следующие простые команды:

ТОР ++;

if (TOP < M)

STORE (TOP)=X(I);

tlse cout << «Переполнение стека»;

Далее для выбора элемента  выполняются следующие команды:

if (TOP)

{

X(I)=STORE(TOP);

TOP - -;

}

tlse cout << «Cтек пуст»;

Рис. 9.  Конфигурации стековой памяти при работе  алгоритма

WELL-FORMED (ПРАВИЛЬНО ПОСТРОЕННАЯ).

2.2.3. Очереди

В  стековой памяти для внесения и удаления элементов можно пользоваться  только словом ТОР. В очереди элементы добавляются с  одного конца, а выбираются с другого. Эти  элементы обычно называются началом (FRONT)  и  концом (REAR) очереди. Термин «очередь» выбран потому, что эти структуры данных часто используются для моделирования обслуживающих линий, например люди в очереди к  парикмахеру, автомобили у светофора, очередь заданий операционной  системы.

Для моделирования очереди, как правило, используют линейный массив [например, QUEUE(500)] и  две целые  переменные FRONT и  REAR , которые указывают на первые и последние элементы очереди соответственно. Вначале  REAR≥FRONT очереди добавится свыше 500 элементов, то, по-видимому, некоторые записи будут удалены из начала очереди. Если это так, то, чтобы не допустить переполнения массива, мы присваиваем REAR=1 и продолжаем заполнять очередь с начала массива. Впрочем, REAR никогда не должен перегонять FRONT.

На рис.10 показано то, что называется ситуацией  одна очередь - одно обслуживание. В этом примере емкость очереди 5, конкретные клиенты помечены  метками от А до Н; первый ожидающий в очереди клиент  обслуживается за три единицы времени, после чего он  покидает очередь. В момент Т=0  очередь пуста, и значения FRONT (F) и REAR(F) равны нулю. В  момент Т=1 прибывает А, ждет 3 единицы времени и покидает очередь в момент Т=4. Клиенты B,C,D,E,G и H  прибывают в моменты времени 2,3,4,7,8 и 9 соответственно. С ждет 4 единицы, прежде чем  продвинуться в начало очереди, и  покидает ее в момент Т=10. Когда прибывает G, в  момент Т=8, конец очереди находится в массиве в положении 5. Здесь мы помещаем G в положение 1 очереди и присваиваем R=1.  Когда в момент Т=9 прибываем Н, в R засылается 2, в этот момент очередь  полностью заполнена. Теперь конец очереди сравнялся с ее началом, и, пока С не покинет очередь,  в нее  становится нельзя.

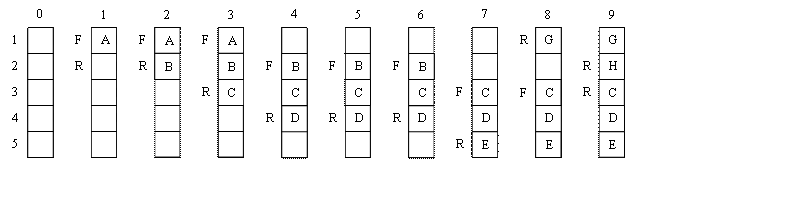
Рис. 10.  Реализация очереди с использованием линейного массива.

2.3. Алгоритмы машинной математики

2.3.1. Сортировка

Сортировка стала  важным предметом вычислительной математики в  основном потому, что она отнимает значительную часть времени работы ЭВМ. Осознание того, что 25% всего времени вычислений расходуется на сортировку данных, придает особое значение эффективным алгоритмам сортировки.

К сожалению, нет  алгоритма сортировки, который был бы наилучшим в любом случае. Трудно даже решить, какой алгоритм будет лучшим в данной ситуации, так как эффективность  алгоритма сортировки может зависеть от множества факторов, например от того:

1.  каково число сортируемых элементов;

2.  все ли элементы могут быть помещены  в доступную оперативную память;

3.  до какой степени элементы уже отсортированы;

4.  каковы диапазон и распределение значений сортируемых элементов;

5.  записаны ли элементы на диске, магнитной ленте или перфокартах;

6.  каковы длина, сложность и  требования к памяти алгоритма сортировки;

7.  предполагается ли, что элементы будут периодически исключаться или добавляться;