Организация расчетных позиций воздушных судов для УВД при взлете и посадке, страница 3

Время полета
№	Д=20 км(мин)	Д=15 км(мин)	Д=10 км(мин)	Д=8 км(мин)
1	3,00	2,17	1,17	0,83
2	3,083	2,167	1,083	0,583
3	3,500	2,583	1,333	0,833
4	3,167	2,167	1,167	0,500
5	2,917	2,250	1,000	0,417
6	2,833	2,083	1,000	0,417
7	3,833	2,667	1,167	0,667
8	2,833	2,000	0,917	0,500

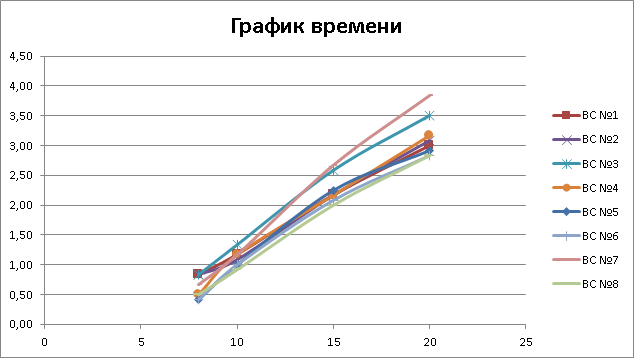
По данным таблицы № 5 построили график времени движения выбранных ранее прилетающих воздушных судов (Рисунок 2).

Затем находится среднее значение времени My(D)

Таблица 6.Значения My(D)

Рис 3. График My(D)

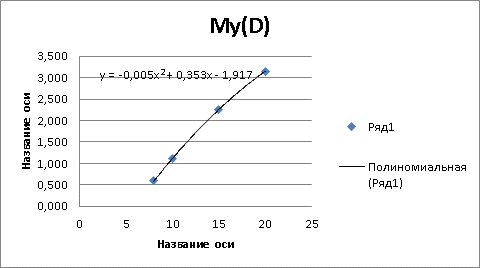
При построении полиномиального графика My(D) получается  уравнение y = -0,005x² + 0,353x - 1,917

Таблица 7.Коэффициенты My(D)

Далее находим стандартное отклонение  σy(D)

Таблица 8.Значения σy(D)

Рис 4.График σy(D)

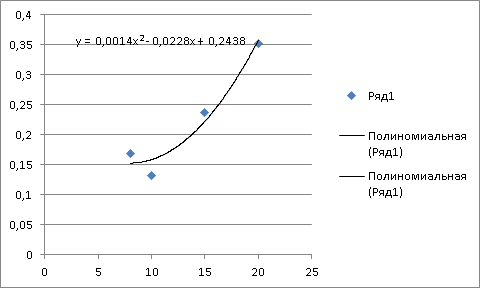
Построив график получится уравнение y = 0,0014x² - 0,0228x + 0,2438

Таблица 9. Коэффициенты σy(D)

Если известна математическая модель для и  например, в виде полинома второй степени:

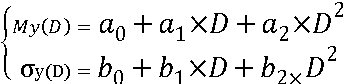
То, подставив значения из таблиц 7 и 9 получим значения  в виде полинома второй степени:

Таблица 10.Значения

Рис.5 График полинома

Тоже самое делаем для :

Таблица 11.Значения

Рис.6 График полинома

Теперь если мы сравним значения таблицы 6,8 и 10,11 то увидим, что они примерно одинаковы, значит, мы все посчитали правильно.

Раздел 5. Расчет допустимых удалений прилетающего вс при выдаче разешения исполнительного влетающему.

Расчетные позиции - это допустимые удаления D прилетающего воздушного судна при котором диспетчер может выдать разрешение исполнительного вылетающему ВС.

                                                          

 

РП – Расчетная позиция

РПР – Рубеж принятия решения

Рубеж принятия решения(L) в наших расчетах мы принимаем равным 6км.

Для того что бы найти требуемое допустимое удаление D для прилетающих ВС используется неравенство:

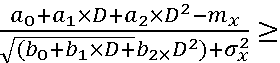1,645

Значения коэффициентов a мы взяли из таблицы 7,а значения b из таблицы 9.

Подставив все члены неравенства, и выбрав D от 8км до 24км мы получили таблицу 10.

Таблица 10.Значения математической модели №2

	DH8D	SU95
Д	ММ№2
8	-2,069582142	-1,894994713
9	-1,575955859	-1,422420827
10	-1,097132561	-0,964671073
11	-0,639472694	-0,527316379
12	-0,208416519	-0,115134805
13	0,191791427	0,268113276
13,58	0,408570526	0,476054455
13,63	0,426712344	0,493470264
15	0,889276068	0,938390279
16	1,1844942	1,223415254
17	1,44442128	1,475246904
18	1,67034893	1,694948471
19	1,864098977	1,884081133
20	2,027825447	2,044533753
21	2,16385179	2,178378899
22	2,274545743	2,287758717
23	2,362229138	2,374799782
24	2,429117363	2,441553437

Методом подбора мы получили значение для DH8D и SU95  D=18 при k=1,645.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1.  http://airkhv.ru/ Сайт аэропорта Владивосток

2.  https://ru.wikipedia.org

3.  http://www.caiga.ru/

4.  Конспект лекций по дисциплине Проектирование ВП, В.И.