Расчет напряженно-деформированного состояния инструмента при заданных условиях обработки, страница 4

По данным таблицы из выданного задания  при изменении одного из режимных параметров, остальные остаются неизменными, значит коэффициенты в формуле зависимости сможем найти используя однофакторную методику, то есть отдельно определять зависимость температуры в зоне резания поочередно от глубины резания, подачи и скорости резания. На основании этого формула зависимости температуры в зоне резания будет выглядеть

                                                 (2.1)

Коэффициент  найдем

                                                   (2.2)

Нахождение коэффициентов  и показателя степени  такой функции при экспериментальных исследованиях упрощается после логарифмирования: ln(θ)=ln(C_θ)+x_θ∙ln(v). Значения ln(θ) и ln(v) приведены в таблице 4.

№ опыта	ln(v)	ln(θ)
1	4,0993	5,51
2	4,399	5,557
3	4,7	5,899
4	5,0998	5,950
5	5,299	6,178

Таблица 4 – Значение натуральных логарифмов для температуры в зоне резания и скорости резания.

Коэффициент  равен тангенсу наклона линий функции θ= f(v) к горизонтальной оси.   Полученные выражения аналогичны уравнениям первой степени вида

Для нахождения  требуемой функции воспользуемся методом наименьших квадратов. Его суть в том, чтобы найти коэффициенты линейной зависимости при которых функция принимает наименьшее значение, то есть при данных a и b квадраты отклонений экспериментальных данных от найденной прямой будут наименьшими. Коэффициенты a и b линейной функции найдем решив систему уравнений  по формуле (2.3) [4, стр. 123].

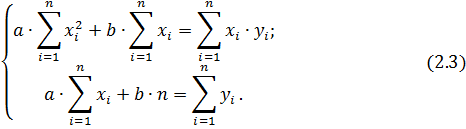
Примем ln(v)=x, а ln(θ)=y, тогда рассчитаем , получим следующие значения

соответственно

.

Так же рассчитаем  и . Для нахождения всех необходимых коэффициентов формулы (2.3) найдем  . Подставим найденные коэффициенты в формулу (2.3)

Решив систему уравнений получим a=0,5494; b=3,226. Уравнение линейной аппроксимации будет выглядеть следующим образом: ln(θ)=0,5494∙ln(v)+3,226. Построим данную прямую, и отметим точки из таблицы 4 [ПРИЛОЖЕНИЕ 3].

Угол наклона данной прямой равен 28̊, а tg(28̊)=0,532=> z_θ=0,532.

Подставив значения скорости резания и температуры в зоне резания в формулу (2.2) получим

Среднее значение коэффициента С_θ =27,414.

При однофакторной методике расчета зависимость температуры в зоне резания от подачи будет выглядеть

                                             (2.4)

а коэффициент С_θ определяться по формуле (2.5)

 .                                             (2.5)

Как и в предыдущем случае логарифмируем значения подачи и температуры в зоне резания для получения упрощенной модели зависимости- ln(θ)=ln(C_θ)+y_θ∙ln(s). Значения ln(θ) и ln(s) приведены в таблице 5.

№ опыта	ln(s)	ln(θ)
1	-1,272	4,32
2	-1,0788	4,591
3	-0,843	4,71
4	-0,653	5,164

Таблица 5 – Значение натуральных логарифмов для температуры в зоне резания и подачи.

Коэффициент  равен тангенсу наклона линий функции θ= f(s) к горизонтальной оси.   Полученные выражения аналогичны уравнениям первой степени вида

.

Найдем коэффициенты уравнения решив систему уравнений (2.3).

Примем ln(s)=x, а ln(θ)=y, тогда рассчитаем , получим следующие значения