Дано:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
![]() ;
;
![]() .
.
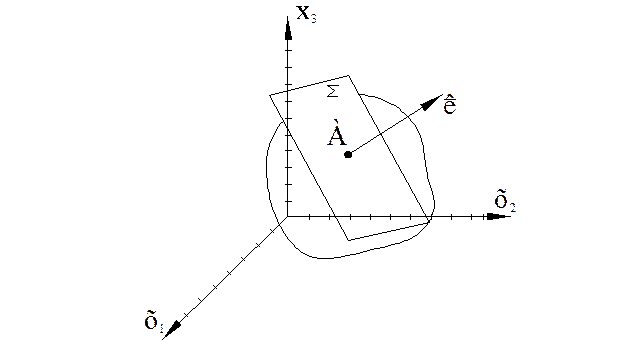
Задание:
1) Найти вектор
напряжений ![]() , отнесенный к плоскости
, отнесенный к плоскости ![]() .
.
2) Найти нормальную
и касательную составляющие вектора напряжений, отнесенные к плоскости ![]() .
.
3) Найти главные напряжения.
4) Определить
направляющие векторы площадок ![]() , к
которым отнесены главные напряжения.
, к
которым отнесены главные напряжения.
5) Найти максимальное
касательное напряжение (![]() ),
построив диаграмму Мора.
),
построив диаграмму Мора.
6) Найти
нормальное и касательное напряжения по диаграмме Мора при заданных углах![]() и
и ![]() .
.
7) Найти интенсивность напряжений в точке А.
8) Определить состояние материала в точке А, т.е. состояние деформации.
9) Найти главные деформации в точке А.
10) Найти интенсивность деформации.
11) Проверить выполнение условия не сжимаемости в точке А.
12) Вычислить показатель напряжённого состояния.
Решение:
1. Находим вектор напряжений ![]() .
.
1.1. Нормирование вектора
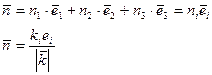
![]()
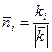
![]() ;
;
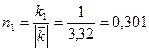 ;
; 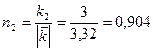 ;
; 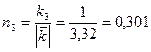 .
.
1.2. Нахождение ![]() .
.
![]() ;
;
![]() ;
;
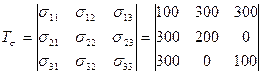 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2. Находим нормальную и касательную составляющие вектора напряжений.
![]() ;
;
![]()
![]() ;
;
![]() .
.
3. Находим главные напряжения.
![]() ;
;
![]() ;
;
В покомпонентном представлении
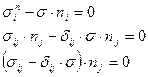
![]() Получаем систему
Получаем систему 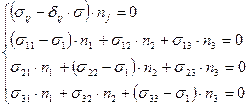 .
.
Нетривиальное решение системы можно обеспечить, если выполняется условие:
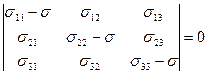 ;
;
![]() ; - уравнение Гамильтона – Кэли.
; - уравнение Гамильтона – Кэли.
![]() ;
;
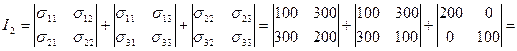
![]() ;
;
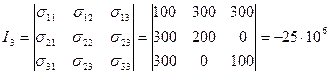 .
.
Уравнение Гамильтона-Кэлли может быть сведено к приведённому кубическому уравнению с помощью подстановки:
![]() ;
;
![]() , где:
, где:
![]() ;
;
![]() ;
;
Решение приведённого уравнения
![]() , существует при Р3+Q2<0.
, существует при Р3+Q2<0.
Для него решение Кардано представляется в тригонометрическом виде:
![]() ;
;
![]() ;
;
![]() ;
;
где: 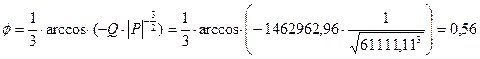 .
.
Определяем ![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Проверяем правильность определения главных напряжений:
![]() ;
;
![]() ;
;
![]() .
.
4.Находим
направляющие вектора![]()
а)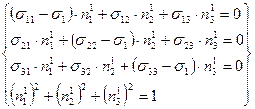
![]()
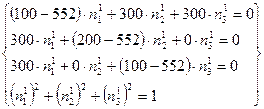
![]()
![]()
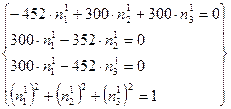
![]()
![]()
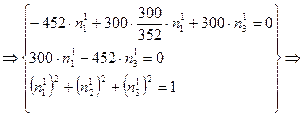
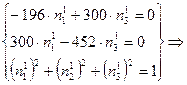
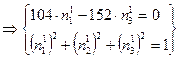
![]()
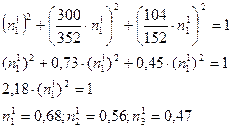
б)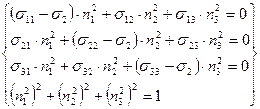
![]()
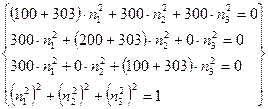
![]()
![]()
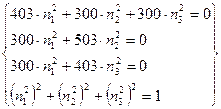
![]()
![]()
![]()
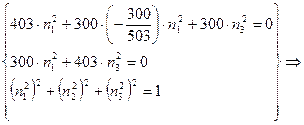
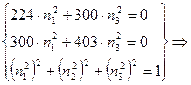
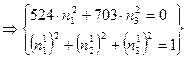
![]()
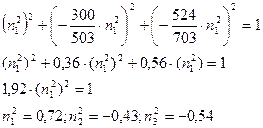
в) 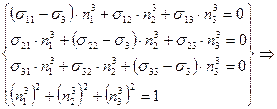
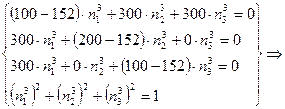
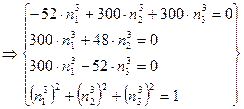
![]()
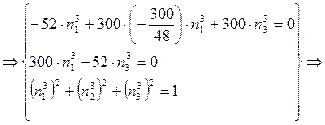
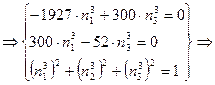
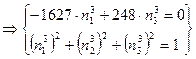
![]()
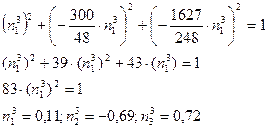
5. Построение диаграммы Мора.
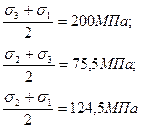
![]()
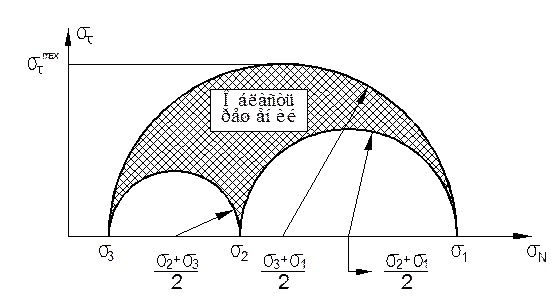
6. Нахождение по диаграмме Мора ![]() и
и
![]() , при заданных
, при заданных ![]() и
и ![]() .
.
![]() ;
; ![]()
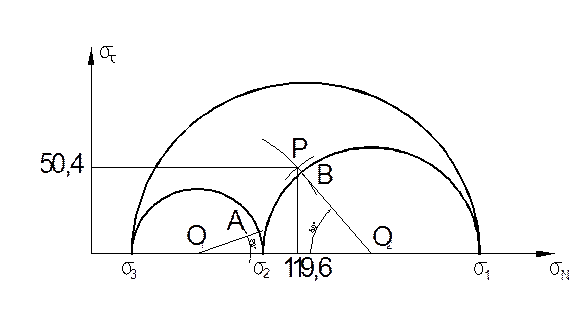
7.Интенсивность напряжений.
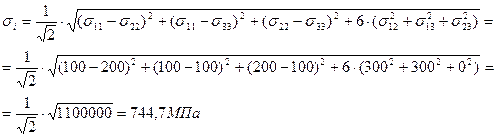
8.Определяем состояние материала.
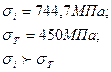
![]() состояние материла – пластическое.
состояние материла – пластическое.
9. Находим главные деформации ![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
10.Находим интенсивность деформаций.
![]() ;
;
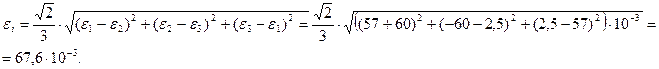
11. Проверка условия не сжимаемости.
![]() ;
;
![]() -
условие не сжимаемости выполняется.
-
условие не сжимаемости выполняется.
12.Вычисляем показатель напряжённого состояния.
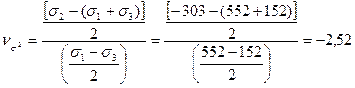 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.