Математика \ Дискретная математика

Визуальный метод минимизации булевых функций. Упрощение троичных матриц, страница 5

Обозначая, как и раньше, через М* множество элементов из М¹, не покрытых выбранной допустимой совокупностью А⁺, будем говорить, что интервал U_j поглощает интервал U_i , на множестве М*, если любой элемент из М*, принадлежащий интервалу U_i, принадлежит и интервалу Uj.

В основе описываемого здесь метода построения допустимой совокупности лежит следующее утверждение:интервалUj, может быть передан из множества А* в множество А^-, если в множестве А* существует некоторый другой интервал U_j, который поглощает U_i; на множестве М*.

Условия возможной передачи интервала U_i, из множества А* в множество А* остаются прежними: он не должен покрываться совокупностью остальных интервалов, принадлежащих объединению множеств А⁺ и А*.

Поскольку при передаче некоторого интервала из множества А* в множество А^- происходит сокращение множества А*, это может позволить найти затем в множестве А* другой интервал, который можно передать множеству А⁺. В свою очередь передача некоторого интервала в множество А⁺может создать условия для последующего сокращения текущего остатка А*. В этом и заключается цепной характер описываемого процесса.

Представляя множества А⁺, А^- и А* в матрице U, будем разбивать ее в текущей ситуации на три части — строчные миноры, обозначаемые соответственно через U⁺, U^- и U*. В процессе построения допустимой совокупности матрицы U⁺ и U^- будут расти, а матрица U* — сокращаться.

Строку u_i матрицы U* можно передать в матрицу U^-, если в матрице U* останется некоторая другая строка u_j; такая, что будет вырожден минор, образуемый пересечением строки u_j, а также неортогональных строке u_iстрок матрицы U*, со столбцами, в которых строка u_i, имеет значение «—».

Строка и; матрицы U* передается в матрицу U*, если не будет вырожден минор, образуемый пересечением неортогональных строке и; строк матриц U* и U* со столбцами, в которых строка и; имеет значение «—».

Пример. Обратимся к рассмотрению конкретного примера, чтобы продемонстрировать на нем описанные процессы упрощения троичных матриц. Пример этот, довольно сложный, просчитан на ЭВМ.

Заметим, что демонстрируемые матричные преобразования будут иногда сопровождаться эффектом перемешивания строк матрицы, что явилось побочным следствием повышения эффективности реализуемых на ЭВМ алгоритмов.

Пусть исходная матрица U задает некоторую ДНФ:

Строя для каждой строки этой матрицы соответствующий ей минор, образуемый из неортогональных или смежных с ней строк, находим все обязательные максимальные интервалы. Их оказывается пять и они отмечены в матрице знаком +. Например, строке 010 - - 01 соответствует минор

который оказывается невырожденным (существует ортогональный ему вектор 0 0), в связи с чем эта строка обязательна.

К сожалению, большинство строк не обязательно. Поэтому, чтобы применить итеративную процедуру построения допустимой совокупности интервалов, получим предварительно множество А всех максимальных интервалов множества М¹ (например, методом Блека—Порецкого). Кроме интервалов, перечисленных в исходной матрице U, в множество А войдут также следующие интервалы:

Последующее разложение множества А на три части приводит к получению допустимой совокупности A⁺

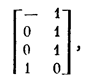представленной матрицей

(первые пять ее строк задают найденное ранее ядро решения), и несокращаемого далее текущего остатка А*, представленного матрицей

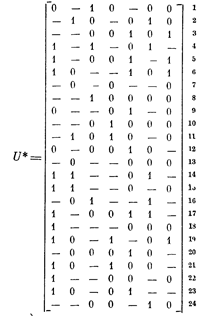(нумерация строк этой матрицы понадобится нам в дальнейшем). Остальные максимальные интервалы войдут в множество А^-, представляемое матрицей U^-, которую

1 2 3 4 5

Скачать файл