В связи с этим несомненный практический интерес представляют методы непосредственного преобразования произвольной троичной матрицы U к некоторой минимальной форме, без предварительного получения булевой матрицы В.
Устранение избыточности. Простейшие методы минимизации ДНФ строятся на устранении избыточности в ней и работают в соответствии с определением понятия безызбыточности. При этом полагается, что безызбыточная ДНФ будет служить приемлемым приближением к оптимальной форме. Под оптимальной мы будем по-прежнему считать кратчайшую ДНФ.
По определению ДНФ безызбыточна, если из нее нельзя удалить ни одного члена и ни одной буквы в каком-либо члене. Другими словами, троичная матрица U безызбыточна, если из нее нельзя удалить ни одной строки и нет такого элемента в матрице, обладающего значением 0 или 1, чтобы это значение можно было заменить на «—», получив при этом матрицу, эквивалентную исходной.
Введем две операции упрощения матрицы U, основанные на том определении: выбрасывание строки и выбрасывание буквы. Строка Ui матрицы U выбрасывается, если представляемая матрицей U булева функция при этом не изменяется. Выбрасыванием буквы мы будем условно называть операцию смены значения некоторого элемента Ui матрицы U с 0 или 1 на «—», если это возможно.
Очевидно, что строку щ матрицы U можно выбросить лишь в том случае, если любой поглощаемый ею булев вектор поглощается в то же время еще какой-то строкой. матрицы U. А это условие легко трансформируется в следующее: минор, образуемый пересечением строк, неортогональных строке и,, со столбцами, в которых строкаUt имеет значение «-», должен быть вырожден.
Действительно, если этот минор не вырожден, то найдется некоторый ортогональный ему булев вектор. Заменив значениями его компонент значения «—» соответствующих компонент строки Ui, мы получим булев вектор, поглощаемый строкой и, и не поглощаемый более ни одной строкой матрицы U. Очевидно, что в этом случае строку и, выбрасывать нельзя. Если же минор вырожден, то не существует такого булева вектора, который поглощался бы только строкой Ui.
Заменить значение 0 или 1 некоторого элемента иi матрицы U на значение «—» можно только в том случае, еcли будит вырожденным минор, образованный пересечением тех строк, которые не ортогональны троичному вектору, соседнему строкеUi, по компоненте j, с теми столбцами, в которых строка и, имеет значение «—». В самом деле, в этом случае указанный соседний вектор можно добавить в матрицу U и, склеив его со строкойUi, получить требуемый результат.
Пользуясь описанными операциями, мы всегда можем найти безызбыточную ДНФ, исходя из некоторой произвольной. При этом следует помнить, что получаемый результат будет зависеть от порядка выбора как операций, так и строк матрицы U, к которым они применяются. Многошаговый процесс упрощения может иметь цепной характер. Пусть, к примеру,
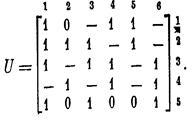 |
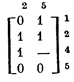
Будем сначала удалять из этой матрицы некоторые строки целиком, если это возможно, а уж во вторую очередь стараться «выбрасывать буквы». В данном случае оказывается, что единственно возможное упрощение такого рода заключается в замене значения элемента и4/5 с 0 на «—». Соответствующий минор оказывается особенным — формально он должен иметь одну строку, образованную из строки 3 матрицы U, и ни одного столбца. Будем считать такого рода минор вырожденным, полагая, что особенный минор противоположного типа, содержащий формально несколько столбцов и ни одной строки, будет невырожденным.
 |
 |
которая оказывается минимальной, соответствуя кратчайшей ДНФ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.