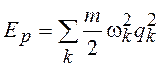Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках, страница 4

.                                         (19.27)

Полная энергия колебаний решетки

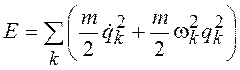.                            (19.28)

Выражение

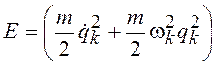.                                (19.29)

совпадает с энергией гармонического осциллятора, уравнение движения которого имеет вид

.                                   (19.30)

Выражение (19.22) является решением этого уравнения. Отсюда следует, что одномерный кристалл, содержащий N атомов и характеризующийся N степенями свободы, можно описать с помощью N нормальных координат. Каждая нормальная координата описывает определенную конфигурацию атомов кристалла, совершающую колебания по некоторому гармоническому закону. Такое колебание называется нормальным колебанием или модой. Произведение массы атома на обобщенную скорость можно рассматривать как обобщенный импульс нормального колебания одномерной решетки.

§ 19.3. Квантование энергии гармонического осциллятора.

Фононы

Запишем уравнение Шредингера для гармонического осциллятора в общем, виде

.                                      (19.31)

Любое состояние осциллятора можно представить как суперпозицию стационарных состояний

,                                        (19.32)

где

,                                          (19.33)

y_n(x) и Е_n - собственные функции и собственные значения оператора Гамильтона.

Совокупность всех амплитуд С_n(х) является волновой функцией в энергетическом представлении. Вероятность обнаружить гармонический осциллятор в момент времени t в состоянии с определенной энергией Е_n

                                          (19.34)

и не зависит от времени. Это соответствует тому, что энергия является интегралом движения, т.е. сохраняющейся величиной.

Амплитуда С_n(х)  изменяется во времени по гармоническому закону с периодом классического осциллятора 2p / w лишь с точностью до фазового множителя e^-iwt/2

.                                  (19.35)

Из условия периодичности амплитуды следует

.                          (19.36)

Отсюда

,          .                      (19.37)

где n =0, 1, 2, 3, ... Заменив  в (19.36) квантованным значением (19.37) и сравнив с (19.33) видим, что энергия квантового осциллятора

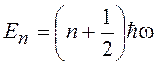.                                          (19.38)

При n = 0 нулевая энергия осциллятора .

Существование нулевой энергии квантового осциллятора является прямым следствием  соотношения  неопределенностей Гейзенберга (см. § 15.1)

.                                     (19.39)

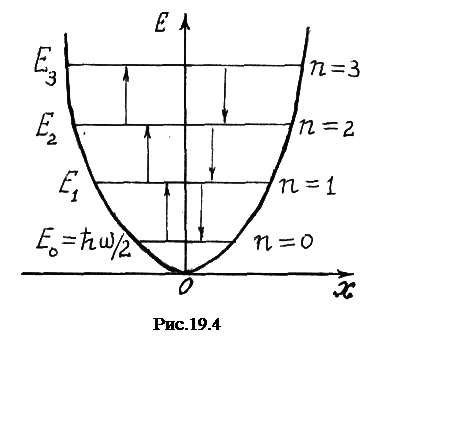
Энергетический спектр квантового осциллятора показан  на рис.19.4.

Поскольку средние значения координаты и импульса осциллятора равны нулю, можно заменить в (19.39)

;  и переписать (19.39) в виде

.          (19.40)

С другой стороны, средняя энергия осциллятора

.                              (19.41)

Заменив  в (19.41), получаем

.                                   (19.42)

Исследуя (19.42) на экстремум, определяем минимальную энергию осциллятора. Из условия  получаем . Подставляя в (19.42), видим, что минимальная энергия осциллятора равна нулевой энергии:

.                                              (19.43)

Квантовый осциллятор может изменять энергию только на величину . Изменение колебательного квантового числа согласно правилу отбора Dn = ±1. Квант энергии  носит название фонона. Импульс фонона . Волновое число k = w / u.

При малых  или при больших l, дисперсия упругих волн отсутствует, так как sin ka/2 » ka/2 и фазовая скорость волны равна групповой скорости. В этом случае зависимость энергии от импульса фонона является линейной

.                                                     (19.44)

Фонон есть единичное квантовое возбуждение определенного нормального колебания. Фонон является квазичастицей, обладающей отличительными свойствами.