Элементы сверхпроводящей электроники. Динамика кристаллической решетки. Магнитные квантовые эффекты в полупроводниках, страница 3

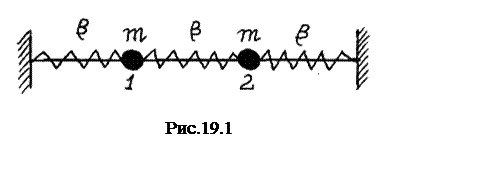
Рассмотрим сначала колебания двух упруго связанных одинаковых тел (рис.19.1). Пусть колебания происходят под действием упругой силы

F = -bS.                         (19.1)

В этом случае уравнения движения тел являются связанными

;                             (19.2)

;                            (19.3)

где S₁ и S₂ - координаты смещения тел.

Складывая уравнения (19.2) и (19.3), получаем первое независимое уравнение гармонического осциллятора

,                                               (19.4)

где q₁ = S₁ + S₂ - нормальная координата, описывающая нормальное колебание (рис.19.2). Собственная частота гармонического осциллятора

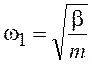  .                                                    (19.5)

Решение уравнения запишем в комплексной форме

.                                              (19.6)

Вычитая уравнение (19.3) из (19.2), получаем второе независимое уравнение гармонического осцил-лятора

,    (19.7)

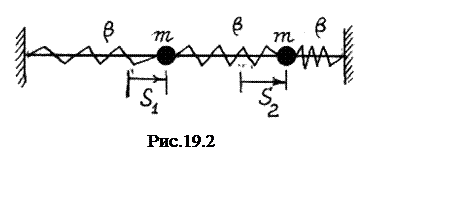
где q₂ = S₁ - S₂ - нормальная координата, описывающая второе нормальное колебание (рис.19.3). Тела движутся навстречу друг другу. Осциллятор совёршает нормальное колебание с собственной частотой

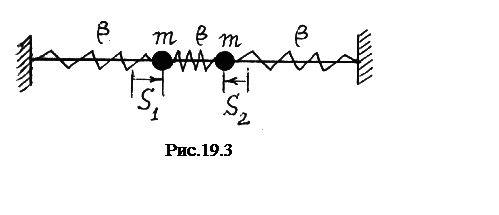
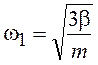 .                (19.8)

Решение уравнения (19.7) можно записать в комплексной форме без начальной фазы

.         (19.9)

Из (19.6) и (19.9) видно, что каждая нормальная координата гармонически зависит от времени.

Определим энергию системы. Представим нормальные координаты в виде

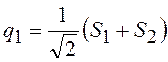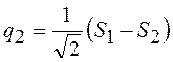;           .                             (19.10)

Соответственно обобщенные скорости

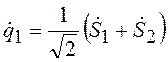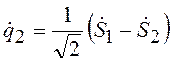;          .                             (19.11)

множитель 1/ выбран для удобства. Тогда смещения S₁ и S₂ имеют вид

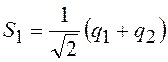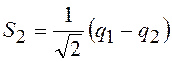;          .                             (19.12)

Выразим кинетическую E_c и потенциальную E_p энергии через нормальные координаты q₁ и q₂ и обобщенные скорости  и .

Кинетическая энергия

.                                         (19.13)

Возведя в квадрат и сложив соотношения (19.11), имеем равенство

.                                      (19.14)

Тогда

.                                         (19.15)

Потенциальная энергия

.                             (19.16)

Возводим (19.12) в квадрат и складываем:

.                                      (19.17)

С учетом (19.12), (19.17), (19.6) и (19.9) преобразуем (19.16)

.                            (19.18)

Энергия системы в нормальных координатах

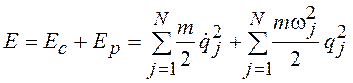.                      (19.19)

В данном случае N = 2.

§ 19.2. Нормальные колебания одномерной решетки

В § 9.1 мы рассмотрели колебания и волны в цепочке N одинаковых атомов и показали, что смещение n-то атома имеет вид бегущей волны

          S_n = Ae^i(nka-wt),                                               (19.20)

когда выполняется дисперсионное соотношение (9.7). Применяя условие цикличности, согласно которому S_n = S_n+N мы получили, что волновой вектор  меняется дискретно и в интервале от -p/а до p/а имеет N значений k = 2p l /Na, где -N/2 £ l £ N/2.

Гармонические волны (19.20) не описывают наиболее общего случая колебания атомов цепочки. Произвольное движение атомов решетки может быть представлено посредством линейной суперпозиции бегущих волн типа (19.20). Каждая из этих волн характеризуется волновым числом k = 2p/l, = w_k /u. В общем случае смещение n-го атома имеет вид

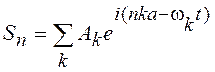.                                (19.21)

fe Нормальные координаты линейной атомной цепочки

,                                  (19.22)

где . Множитель  выбран для удобства. Преобразуем (19.21) с учетом (19.22):

.                                    (19.23)

Заметим, что (19.23) аналогично выражению (19.12) для S₁. Кинетическая энергия одномерной решетки

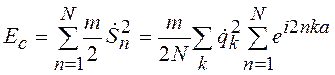.                      (19.24)

Заменяя k = 2pl / Na, можно убедиться в том, что

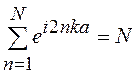.                                              (19.25)

Тогда кинетическая энергия атомов одномерной решетки

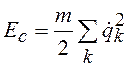.                                              (19.26)

Потенциальная энергия решетки