Комплексные числа. Сопряженные числа. Применение комплексных чисел в геометрии и тригонометрии, страница 5

§8. Применение комплексных чисел в геометрии и тригонометрии

Применение №1

Задача ставится так: вычислить 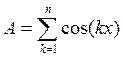 и 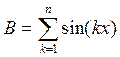. Рассмотрим число . . 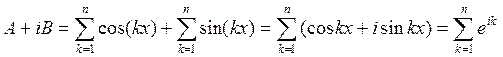Последняя сумма является суммой геометрической прогрессии с первым членом  и знаменателем . Формула этой суммы остается верной и для прогрессии из комплексных чисел, поэтому 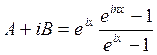. В выражении для  вынесем в числителе за скобки , а в знаменателе . Получим 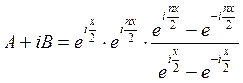. Теперь заметим, что  .  В последнем выражении заменим числитель и знаменатель по этому равенству. Наконец, 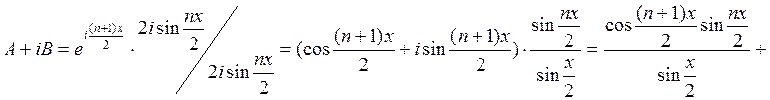 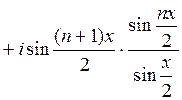. Понятно, что вещественная часть этого числа равна , а мнимая - , откуда 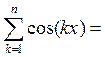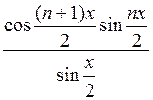, 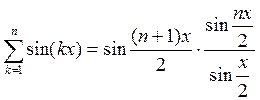. Этим задача решена.

Применение №2

А теперь давайте выразим  и  через  и . Предварительно заметим, что 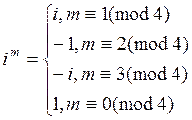В следующих вычислениях был использован бином Ньютона. 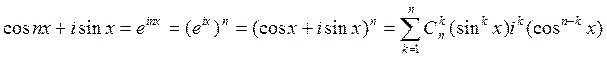. Посмотрим на последнее выражение. При  , что входит в вещественную часть со знаком +. При  такое число входит в вещественную часть со знаком -. Отсюда . При  , что входит в мнимую часть со знаком +. При  , что входит в мнимую часть со знаком -. Вот мы и видим, что . Осталось проверить наши формулы на деле. Ну давайте выведем формулы «упятеренного» угла. , .

Применение №3

Теорема Птолемея. Пусть дан четырехугольник, вписанный в окружность. Тогда произведение длин его диагоналей равно сумме произведений длин его противоположных сторон.

Доказательство. Нарисуем наш четырех угольник на комплексной плоскости, так чтобы центр описанной окружности был совмещен с началом координат, а одна из вершин лежала на вещественной оси.

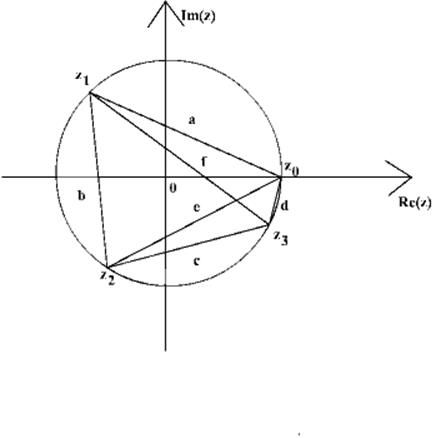
Положим, что радиус окружности равен . Тогда . Теперь стороны и диагонали можно записать как модули разностей векторов. , , , , , . Нам надо доказать, что . Подставим в это равенство наши выражения для сторон и диагоналей и сократим на . Остается доказать, что  . Теперь произведем простое преобразование над первым слагаемым и заменим его на . Мы знаем, что  и  (т.к. ). Тогда первое слагаемое превращается в 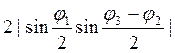. Заметим, что 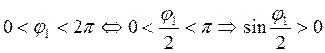. Аналогично 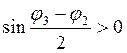. Поэтому первое слагаемое превращается в 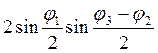. Последнее раскроем по формуле из тригонометрии, получим 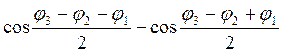. Проделаем аналогичные операции для остальных произведений. Видим, что доказываемое утверждение равносильно 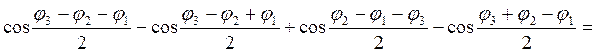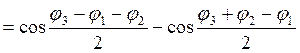. Во-первых, , поэтому второе и третье слагаемые в сумме в левой части сокращаются. После этого левая и правая части совпадают посимвольно. Поэтому теорема Птолемея верна.

Применение №4

Задача. На сторонах треугольника во внешнюю сторону построены квадраты. Доказать, что отрезок, соединяющий центр одного из квадратов с противолежащей вершиной треугольника, равен и перпендикулярен отрезку, соединяющему два центра других квадратов.

Доказательство. 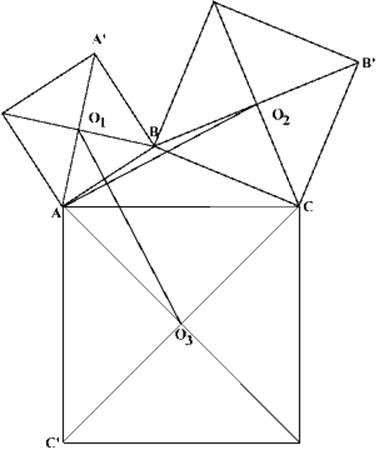Как мы уже говорили, комплексные числа можно рассматривать как вектора. Тогда модуль комплексного – это длина соответствующего вектора, сумма или разность комплексных чисел – это сумма или разность их векторов, а перпендикулярность двух векторов равносильна тому, что один получается из другого домножением на мнимую единицу. На нашей картинке примем  за центр координат (направление осей нас не волнует – оно может быть произвольным). Примем вектор  за комплексное число , а вектор  за . Нас интересуют вектора  и . Выразим их через  наши комплексные числа. , , , , 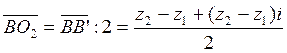наконец, 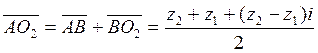. Аналогично выразим . . 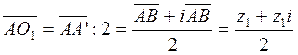. 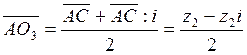Наконец 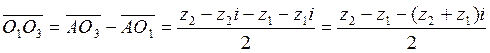. Во-первых, сходу видим, что , откуда следует, что . Так же очевидно, что модули рассматриваемых векторов равны, что означает, что . Что и требовалось доказать в задаче.