Комплексные числа. Сопряженные числа. Применение комплексных чисел в геометрии и тригонометрии, страница 3

Итак, случай первый. Рассмотрим уравнение . Для решения предположим, что . Тогда . Таким образом, модуль неизвестного мы уже нашли. Заметим, что . Это следует непосредственно из нашего переобозначения (когда мы переходили из тригонометрической формы записи в показательную). Отсюда легко найти аргумент неизвестного: 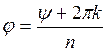. Но таким образом мы получаем бесконечное множество решений. Докажем что их конечное количество, а именно . Разобьем множество целых чисел на классы  следующим образом: к классу  отнесем все числа, кратные , к классу  отнесем все числа, дающие остаток 1 при делении на , т.е. представимые в виде , и так далее, в класс  попадут все числа вида . Теперь возьмем два числа  и  из класса  и подставим их поочередно вместо  в формулу для аргумента неизвестного. Наша цель заключается в том, чтобы доказать, что при такой подстановке получается один и тот же аргумент. Тем самым, мы докажем что корней не более чем  (поскольку классов ровно столько). Действительно 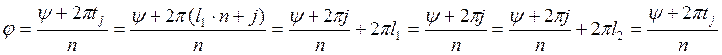 . Что и требовалось доказать. Таким образом, мы видим, всего существует не более  корней (т.к. классов чисел, для которых решения совпадают, не более чем ). Чтобы доказать, что корней ровно , докажем, что для любых двух чисел из разных классов получающиеся из них аргументы не равны. Возьмем на этот раз  и . Проверка для них делается так же, как мы только что делали, и приводит нас к противоречию. В итоге мы видим, что для получения всех решений исходного уравнения достаточно подставить .

Второй случай уравнений с комплексными числами – это квадратные уравнения с комплексными коэффициентами. Разберем этот случай.

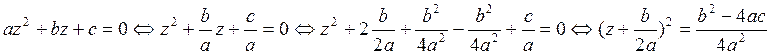 Введем новую переменную 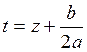. Тогда наше уравнение сводится к виду 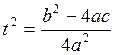, где справа стоит комплексное (или иногда вещественное число). На этом хочется остановиться, сказать, что у этого уравнения два корня, и, следовательно, 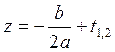. Но давайте чуть-чуть порассуждаем. Если 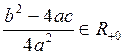, то наше квадратное уравнение сводится к обычному вещественному. Его корни следует считать по формуле 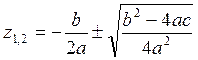. При этом знаменатель из под корня выносить нельзя, т.к. числитель не обязательно является вещественным числом. Вы уже знаете, что корни из комплексных чисел извлекать нельзя. Кстати, сравнивать комплексные числа тоже нельзя. Но продолжим рассуждать. Если 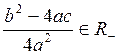, то 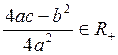. Наше уравнение принимает вид 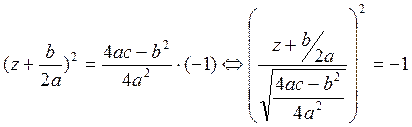. Решим уравнение . Угадывая корни , мы говорим, что уравнение второй степени имеет ровно два корня, поэтому это все корни уравнения . 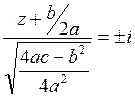Отсюда мы имеем , откуда выводим 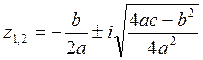. Но если нам совсем не повезло, и 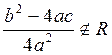, то придется решать квадратное уравнение наичестнейшим образом через базовый алгоритм.

На этом решение уравнений в комплексных числах мы закончим. Конечно, есть еще масса интересного вроде кубических уравнений и много другого, но мы этот материал оставим за его сложностью.

§6. Первообразные корни

Def. Первообразным корнем степени из 1 называется корень уравнения  , который не является корнем уравнения .

Теорема 1. Пусть - первообразный корень ой степени из 1. Тогда - все корни уравнения .

Доказательство. Мы знаем, что всего у нашего уравнения  корней. Если мы хотим доказать, набор из  чисел – это все корни, то нам достаточно показать, что во-первых, каждое из этих чисел – корень, во-вторых, все эти числа равны. Докажем первое утверждение:  , что и требовалось доказать. Второе утверждение не менее очевидно: пусть для неких  . Тогда имеем . Произведение двух комплексных чисел равно нулю тогда и только тогда, когда хотя бы одно из них равно нулю. В нашем случае , значит . Очевидно, что . Но тогда последнее равенство противоречит тому, что - первообразный корень ой степени из 1. Поэтому все степени  различны между собой, а значит, представляют собой набор всех корней уравнения . Этим теорема доказана.