220400 Математический анализ Толстиков А.В.
Курс 1. Семестр 1. Лекция 5. Числовая последовательность и ее предел
1. Числовая последовательность и свойства последовательностей.
2. Предел числовой последовательности и его свойства. Бесконечно малая и бесконечно большая последовательности.
3. Арифметические свойства пределов.
4. Переход к пределу в неравенствах.
5. Теорема о существовании предела монотонной ограниченной последовательности. Число e.
6. Теорема Больцано-Вейерштрасса. Критерий Коши.
Литература: Ильин В.А., с.58-88. Письменный Д., с. 107-111. Ермаков В.И., с.179-180. Архипов Г.И., Садовничий В.А., Чубариков В.Н. , с.30-54.
1. Числовая последовательность и свойства последовательностей.
Определение 1. Числовой последовательность или просто последовательность называется функция f определенная на множестве натуральных чисел N, значения которой числа (действительные или комплексные).
Значение функции в точке n Î N обозначаем символом xn=f(n). Последовательность обозначаем через ее значения : x1, x2, x3,…, xn,… или кратко {xn}. Последовательности задаются следующими способами:
1. Формулой общего члена
последовательности. Например, равенства xn=n2, yn=1/n2 ,
zn= (-1)n , un= c
задают соответственно последовательности {1, 4, 9,…, n2,…}, 
, {-1, 1, -1,…, (-1)n,…}, { c, c, c,…, c,…}. Последняя последовательность называется постоянной.
2. Рекуррентными соотношениями. Например, последовательность чисел Фибоначчи задается соотношениями F1 = 1, F2 = 1, при n>2, Fn= Fn-1 + Fn-2.
Последовательностями являются арифметическая прогрессия {an} и геометрическая прогрессии {bn}, заданные соответственно рекуррентными соотношениями: a1 = a1, при n>1, an= an-1 + d; b1 = b1, при n>1, bn= bn-1q. Арифметическую и геометрические прогрессии можно также задать формулами общего члена: an= a1 + d (n -1), bn= b1qn-1.
Определение 2. Суммой числовых последовательностей {xn}, {yn}называется последовательность {xn+ yn}. Разность, произведение и частное (yn ¹0) этих последовательностей определяются соответственно по формулам: {xn- yn}, {xn yn}, {xn/ yn}.
Определение 3. Последовательность{xn}называется ограниченной сверху, если найдется такое число a, что для любого члена последовательности выполняется неравенство xn £ a.
Последовательность{xn}называется ограниченной снизу, если найдется такое число b, что для любого n Î N выполняется неравенство xn ³ b.
Последовательность {xn}называется ограниченной, если найдется такое число c, что для любого n Î N выполняется неравенство |xn |£ c.
Последовательность {xn}называется неограниченной, если для любого числа c найдется такое число n Î N, что выполняется неравенство |xn | > c.
Определение 4. Последовательностей {xn}называется возрастающей (неубывающей, убывающей, невозрастающей, если для любого n Î N выполняется неравенство xn< xn+1 (соответственно xn£ xn+1, xn> xn+1 , xn³ xn+1).
2. Предел числовой последовательности и его свойства. Бесконечно малые и их свойства.
Определение 1. Число a называется пределом последовательности {xn}, если для любого положительного числа e найдется такое число n0 Î N, что для всех n > n0 выполняется неравенство
|xn - a | < e. (1)
В этом случае говорим, что
последовательность {xn} имеет
предел a ( или xn стремится к a или
последовательность {xn} сходится к a), и
обозначаем 
.
Кратко последнее определение можно записать символически:
.
Если последовательность не имеет предела, то она называется расходящейся последовательностью.
Неравенство (1) равносильно неравенствам -e < xn - a < e, a -e < xn < a +e, которые показывают, что элемент находится в e -окрестности точки a. Поэтому условие, что последовательность {xn} имеет предел a обозначает, что для любой сколь угодно малой
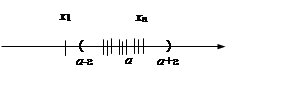e -окрестности точки a все члены последовательности {xn},
начиная с некоторого номера попадут в эту окрестность точки a.
Замечание 1. Постоянная последовательность
un= c, n2 Î N, имеет предел, равный числу c, т.е. 
. Докажите
самостоятельно.
Теорема 1. Если последовательность сходится, то она имеет только один предел.
Доказательство. Допустим, что последовательность {xn} сходится и имеет два предела a и b, a ¹ b. Возьмем число e = |a - b|/2. Так как, то по определению предела существует такое число n1 Î N, что для всех n > n1 выполняется неравенство |xn - a | < e. Аналогично, существует такое число n2 Î N, что для всех n > n2 выполняется неравенство |xn - b | < e. Тогда при n > max{n1, n2} выполняются оба неравенства. Тогда при n > max{n1, n2} получаем противоречие 2e = |a - xn+ xn - b |£|xn - a |+|xn - b |< e+e=2e.
Определение 2. Последовательность{an}называется бесконечно малой, если ее предел равен нулю
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
