Ряды Фурье, интеграл Фурье. Тригонометрические ряды Фурье. Приближение функций многочленами, страница 3

f ^*(t + 2p) = f() = f(+ 2ℓ) = f() = f ^*(t).

Следовательно, f ^*(t) разлагается в ряд Фурье:

f ^*(t) = 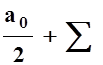a_n cos nt + b_n sin nt,

где     a_n = f ^*(t) cos nt dt,            b_n =f ^*(t) sin nt dt.

Сделаем обратную замену: t = :

f ^*(t) = f(x) = 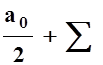(a_n cos + b_n sin),

a_n =.

Аналогичная формула справедлива и для коэффициента b_n.

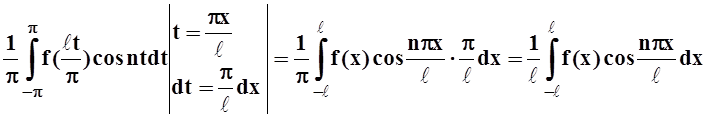Итак, всё сказанное выше справедливо не только для функции с периодом 2p, но и для функции с произвольным периодом T= 2ℓ. Если выполнены условия теоремы Дирихле, то такая функция разлагается в ряд Фурье:

f(x) = 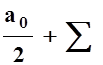(a_n cos + b_n sin), причём коэффициенты находятся по формулам Фурье:

a_n = 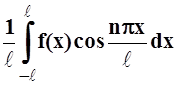,         n = 0, 1, 2, ... ,

b_n = 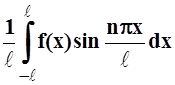,         n = 1, 2, ... .

15.1.4 Ряды Фурье для чётных, нечётных, непериодических функций. Если функция обладает какой–либо симметрией, то техника вычислений при разложении её в ряд Фурье упрощается.

Теорема 4. Если f(x) – чётная функция, удовлетворяющая условиям теоремы Дирихле на отрезке [ – ℓ, ℓ ], то её коэффициенты Фурье можно вычислять по формулам:

a_n =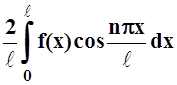,         b_n = 0.

В частности, ряд Фурье чётной функции не содержит синусов. Аналогично, ряд Фурье для нечётной функции не содержит косинусов:

a_n = 0,         b_n =.

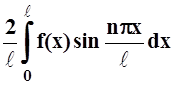Доказательство. Пусть f(x) – чётная. Тогда f(x)sin – нечётная функция, а значит  интеграл по симметричному относительно  0  отрезку равен  0:

b_n =.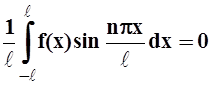

Функция  f(x)cos – чётная, поэтому интеграл по симметричному отрезку [ – ℓ, ℓ ] равен удвоенному интегралу по отрезку [ 0, ℓ ]:

a_n =.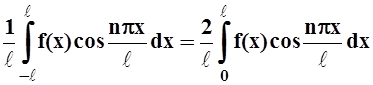

Аналогично получаются формулы для коэффициентов Фурье нечётной функции.

До сих пор мы рассматривали ряды Фурье для периодических функций. Однако любую функцию, определённую на отрезке [a,b],  можно продолжить на всю прямую так, чтобы получилась периодическая функция. Её ряд Фурье будет представлять исходную функцию на отрезке [a,b] (возможно, за исключением граничных точек  a,b).

Пример 2.   Рассмотрим  функцию,  определённую  на  отрезке [–1, 2]  формулой f(x) =x². Имеется много способов построить для неё периодическое продолжение. Пусть f₁(x) – функция, имеющая график

На отрезке [–1, 2] эта функция совпадает с f(x) во всех точках, кроме x= 2. Значение в точке x= 2 приходится считать равным 1, иначе функция не будет периодической. Для функции  f₁(x)  период T= 2ℓ = 3, значит ℓ = 1,5. Разлагая её в ряд Фурье, получим разложение функции  f(x)  на интервале  (–1, 2).  В точках  x= – 1,  x= 2  сумма ряда будет, по теореме Дирихле, равна .

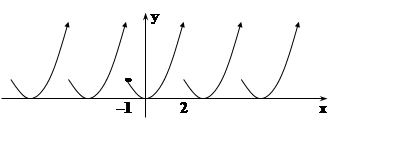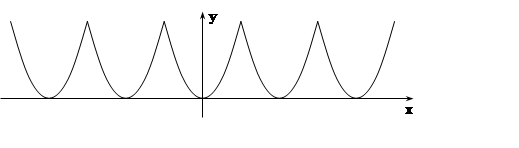Можно рассмотреть другое периодическое продолжение  функции f(x) – функцию  f₂(x) с графиком

Это более удобное продолжение, так как, во–первых, ряд Фурье будет представлять f(x) уже  во всех точках отрезка [–1, 2],  а во–вторых функция  f₂(x)  чётная, её проще разложить в ряд Фурье.

Если функция определена на отрезке [0, ℓ], то её можно продолжить сначала на отрезок [– ℓ, ℓ] так, чтобы она была чётной (или нечётной), а затем продолжить на всю прямую.

Пример 3. Разложить функцию f(x) = 2 – x, определённую на отрезке [0, 2], в ряд Фурье по косинусам.

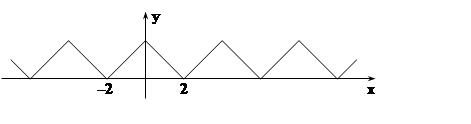Решение. Чтобы получить ряд Фурье по косинусам, нужно, чтобы продолжение f(x) на всю прямую было чётной функцией. Таким продолжением является, например, функция g(x):

Здесь  T= 2ℓ = 4,  поэтому  ℓ = 2.  По теореме 4,   b_n= 0.   Найдём a_n.

a_n = .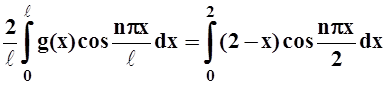

Применим метод интегрирования по частям:

a_n =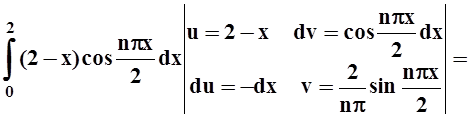

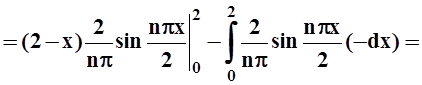
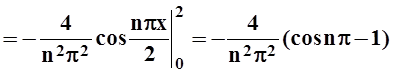
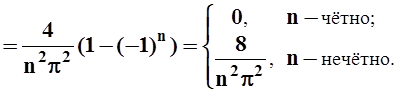
Так как выполнялось деление на  n,  то  a₀  нужно вычислить отдельно:

a₀ =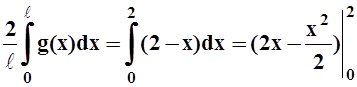 = 4 – 2 = 2.

Осталось записать ответ:

f(x) = 1 +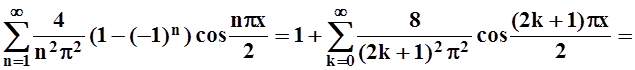

= 1 +.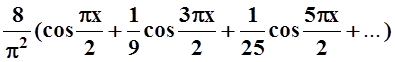

15.1.5 Комплексная форма ряда Фурье. Первое знакомство с комплексными числами у нас состоялось в курсе алгебры. Напомним: комплексное число может быть записано в алгебраической и тригонометрической формах:

z = a + bi = r(cos j+i sin j).

Здесь r==|z| – модуль числа z,   j=argz – аргумент числа z. Было доказано (АГ, 6.1.4) что при умножении чисел их модули перемножаются, а аргументы складываются. Это свойство аргументов комплексных чисел позволяет ввести следующее обозначение:

e^ij= cos j+ i sin j.

Символ e^ij обладает обычным свойством  экспоненты:

.

Мы получаем возможность использовать ещё одну форму записи комплексного числа – показательную:

z = r(cos j+i sin j) = re^ij.