Ряды Фурье, интеграл Фурье. Тригонометрические ряды Фурье. Приближение функций многочленами, страница 2

f(t)dt = dt + (a_ncos nt dt + b_nsin nt dt).

Под знаком суммы все интегралы равны 0, поэтому

f(t)dt = dt = t  =pa₀.

Отсюда следует требуемая формула для a₀:      a₀=f(t) dt.

Умножим обе части равенства (*) на  cosmt:

f(t)cos mt = cos mt + (a_ncos nt cos mt + b_nsin nt cos mt).

Ряд в правой части сходится равномерно. Действительно, равномерная сходимость ряда f_k(t)   к сумме  f(t),  напомним, означает:

"e> 0    $n₀: "n³n₀"t|f_k(t) – f(t) |<e.

Но тогда и для ряда  f_k(t) cosmt это условие выполнено:

"e> 0   $n₀:"n ³ n₀   "t     | f_k(t) cos mt – f(t) cos mt |=

=| f_k(t) – f(t) |×| cos mt |<e.

Следовательно, после умножения на  cosmt,  ряд опять можно почленно интегрировать:

f(t) cos mt dt =

= cos mt dt + (a_ncos nt cos mt dt + b_nsin nt cos mt dt).

Из ортогональности тригонометрической системы функций следует, что все интегралы в правой части формулы равны 0, кроме одного:

f(t)cos mt dt =a_mcos² mt dt = (1 + cos 2mt)dt =

= (t + sin 2mt)=  × 2p=pa_m.

Отсюда следует требуемая формула для a_m:

a_m =f(t)cos mt dt.

Аналогичная формула для b_m получается, если умножать ряд не на cosmt, а на sinmt. Теорема доказана.

Замечания. Если записать произвольный тригонометрический ряд

+ (a_n cos nt + b_n sin nt), гдеa_n,b_n – некоторые числовые коэффициенты, то он может не быть рядом Фурье какой–либо функции (даже если сходится на всей прямой). Если же такой ряд сходится равномерно, то это обязательно ряд Фурье некоторой функции.

С другой стороны, если функция интегрируема на [– p, p] (а для этого достаточно, например, непрерывности), то для неё можно вычислить a_n ,b_n и составить ряд Фурье. Но может оказаться, что он расходится в некоторых (даже во всех!) точках. Возможен также случай, когда ряд Фурье сходится  "t,  но его сумма не совпадает с  f(t). Поэтому важно знать условия, при которых функция  f(t) разлагается в свой ряд Фурье. Достаточные условия содержатся в теореме Дирихле, которую мы приводим без доказательства.

Теорема 3 (теорема Дирихле). Пусть функция f(t) имеет период 2p, причём на отрезке [ – p, p] у неё лишь конечное число экстремумов и лишь конечное число разрывов (все они –  1 рода). Тогда ряд Фурье для f(t) сходится на всей оси, причём его сумма равна

1)  f(t),  если в точке  t функция непрерывна;

2)  ,  если в точке  t функция терпит разрыв.

Здесь   f(t – 0) =f(s),     f(t+ 0) =f(s) – односторонние пределы функции в точке разрыва t.

Пример 1. Разложить в ряд Фурье функцию f(t), период которой равен 2p, если на промежутке ( – p, p] функция задана так:

f(t) =

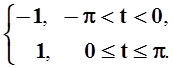
Решение. Построим график функции f(t).

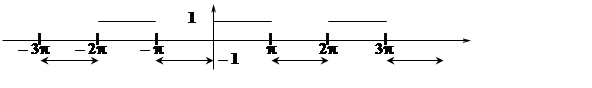
Стрелка на конце линии означает, что концевая точка линии не принадлежит.

Условия теоремы Дирихле, очевидно, выполнены. Поэтомуf(t) разлагается в свой ряд Фурье. Найдём коэффициенты   a_n ,b_n.

a_n =f(t)cos nt dt = (– 1) cos nt dt + 1×cos nt dt =

= – sin nt + sin nt = 0.

Так как на номер  n  приходится делить, то  a₀  нужно вычислить отдельно:

a₀ =f(t)dt = (– 1)dt + dt = ( – t + t) = ( – p+p) = 0.

Вычисление  b_n  аналогично:

b_n =f(t)sin nt dt = (– 1) sin nt dt + sin nt dt =

= (cos nt – cos nt ) = (1 – cos np – cos np+ 1) =

= (1 – cos np)  = (1 – (–1)ⁿ) =

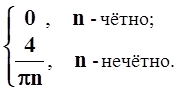
Подставляя найденные коэффициенты в формулу ряда Фурье, запишем ответ:

f(t) = + (a_n cos nt + b_n sin nt) =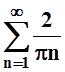 (1 – (–1)ⁿ)sin nt =

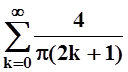= sin (2k + 1)t = (sin t + + + ... ).

По теореме Дирихле, сумма полученного ряда совпадает с f(t) в точках, где f(t) непрерывна. Например, при  t= 10  получим:

(sin 10 + + + ... ) = f(10) = f(10 – 4p) = – 1.

В точках разрыва t=kp сумма ряда, очевидно, равна 0, что совпадает со средним арифметическим односторонних пределов  f(t)  в этих точках.

Интересно проследить, как приближаются частичные суммы полученного ряда к  функции  f(t).  Сделаем это с помощью графиков

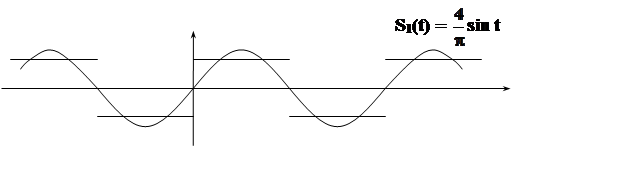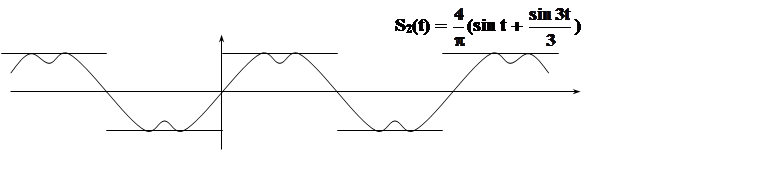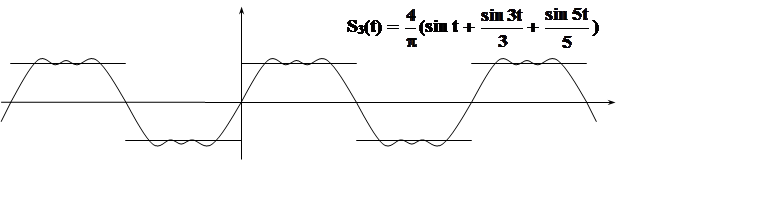Рассмотрим теперь функцию f(x) с произвольным периодом T= 2ℓ. Пусть на отрезке [ – ℓ, ℓ] для неё выполнены условия теоремы Дирихле. Тогда эти условия, очевидно, выполнены  для  функции   f ^*(t) = f()  (полученной  в  результате  замены  переменной  x=), период которой равен 2p: