(f*)* º f.
Аналогично, если f(x) – нечётна, то можно рассмотреть синус – преобразование:
f*(w) =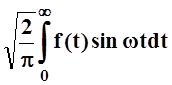 .
.
В этом случае также f(x)
=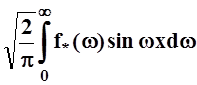 ,
а повторное применение синус – преобразования возвращает к исходной функции: (f*)*
ºf.
,
а повторное применение синус – преобразования возвращает к исходной функции: (f*)*
ºf.
15.5 Задачи с решениями
1. Разложить
в ряд Фурье функцию 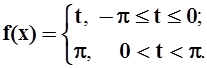
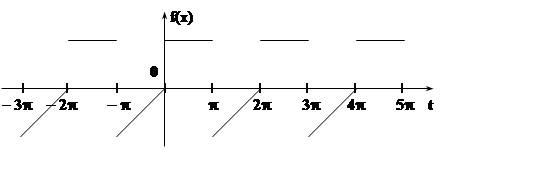 |
Функция, очевидно, удовлетворяет условиям теоремы Дирихле.
Следовательно, разлагается в свой ряд Фурье: f(t)
=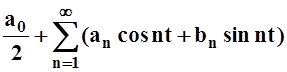 ,
где
,
где
an
= ![]() f(t)
cos nt dt, bn =
f(t)
cos nt dt, bn = ![]() f(t)
sin nt dt, n = 0, 1, 2, 3, 4, … .
f(t)
sin nt dt, n = 0, 1, 2, 3, 4, … .
Найдём коэффициенты:
an=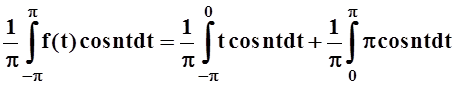 .
.
Второе слагаемое легко вычисляется. Первое слагаемое
интегрируем по частям: u= t,
du= dt, dv= cosntdt,
v= ![]() sinnt. Продолжаем вычисление:
sinnt. Продолжаем вычисление:
an=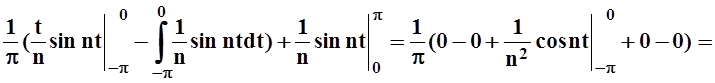
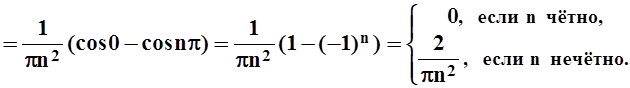
Поскольку приходилось делить на n, то a0 нужно вычислить отдельно:
a0=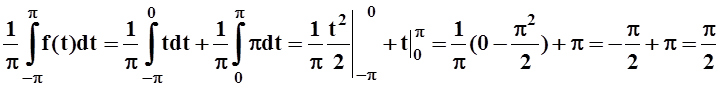 .
.
Вычисляем bn:
bn=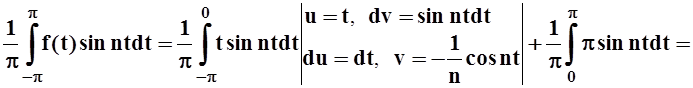
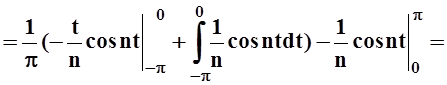
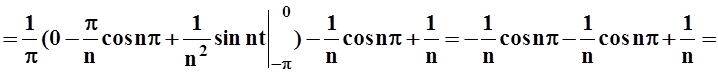
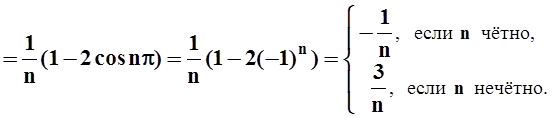
Запишем ответ:
f(t) =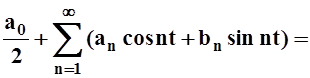
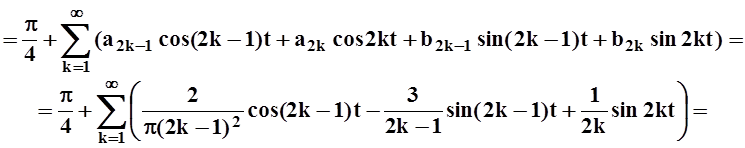
![]()
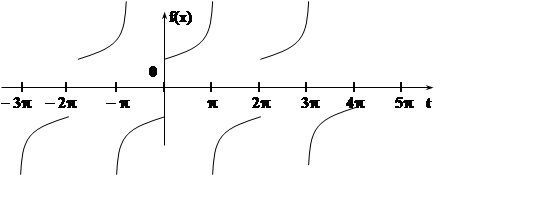
В точках разрыва сумма ряда равна не f(t),
а среднему арифметическому левого и правого пределов: ![]() . В точках 0, ±2p, ±4p,
... сумма ряда равна
. В точках 0, ±2p, ±4p,
... сумма ряда равна ![]() ; в
точках ±p, ±3p,
±5p, ... сумма ряда равна 0.
; в
точках ±p, ±3p,
±5p, ... сумма ряда равна 0.
2. Разложить функцию f(x) = e2x на интервале (0,p) в ряд Фурье по синусам.
 |
Для нечётной функции an= 0. Вычисляем bn:
bn=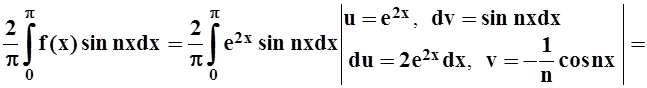
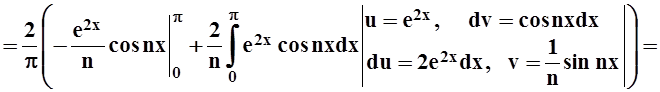
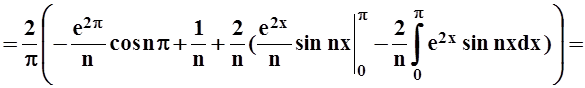
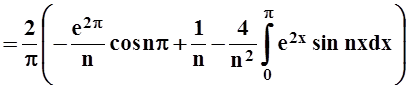 .
.
Получили: 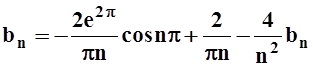 . Находим отсюда bn:
. Находим отсюда bn:
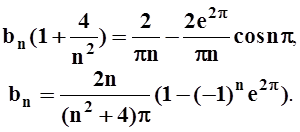
Ответ: 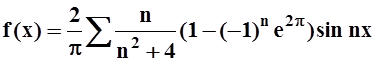 , за исключением точек x= kp. В них сумма ряда
равна 0.
, за исключением точек x= kp. В них сумма ряда
равна 0.
3. Разложить в ряд Фурье функцию f(x) = x– 2, заданную на интервале (7, 13).
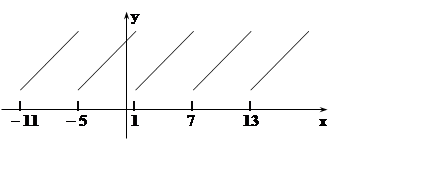 |
Функция разлагается в ряд
Фурье: f(t) =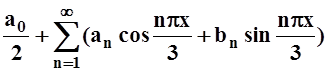 ,
где
,
где
an = 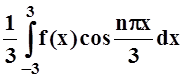 , bn
=
, bn
= 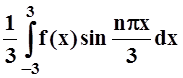 , n = 0, 1, 2, 3, … .
, n = 0, 1, 2, 3, … .
Если периодическая функция с периодом T интегрируется по отрезку длиной T, то результат не зависит от положения отрезка. Здесь нам, конечно, удобнее интегрировать не по отрезку [–3, 3], а по отрезку [7, 13], так как именно на этом отрезке нам известна формула, определяющая f(x).
Вычисляем коэффициенты:
an=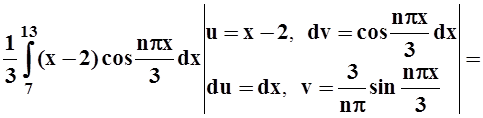
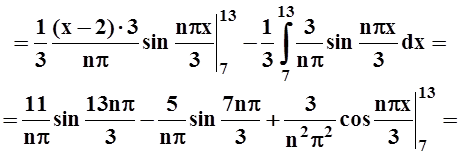
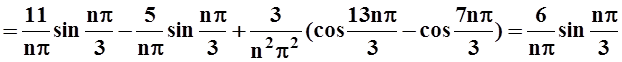 .
.
Мы воспользовались периодичностью синуса и косинуса.
a0 = 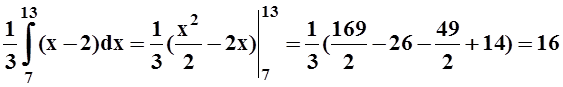 .
.
bn = 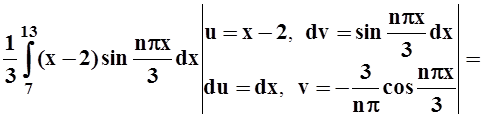
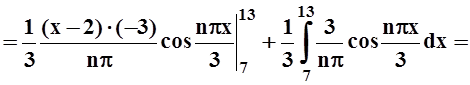
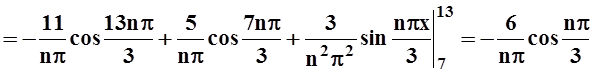 .
.
Ответ: 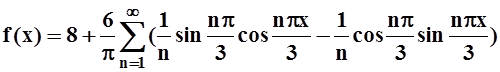 . В
точках разрыва x= 1 + 6k, k= 0,
± 1, ± 2,
… сумма ряда равна 8.
. В
точках разрыва x= 1 + 6k, k= 0,
± 1, ± 2,
… сумма ряда равна 8.
4. Представить функцию f(x) = x2, –4£x£4, рядом Фурье в комплексной форме.
Решение. Если f(x) – периодическая функция с периодом T= 2ℓ, то представление задаётся формулой:
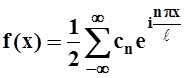 , где
, где 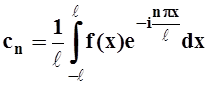 .
.
В нашем случае T= 8, ℓ = 4. При вычислении интегралов можно обращаться с комплексной константой i так же, как с действительными числами. Обоснование этих действий будет дано позже, при изучении комплекснозначных функций. Если появляются какие–либо затруднения в работе с функцией eij, следует обращаться к формуле Эйлера:
eij= cos j+ i sin j.
Найдём коэффициенты cn:
cn = 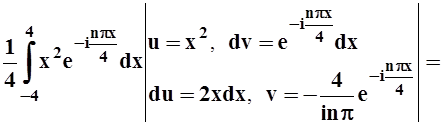
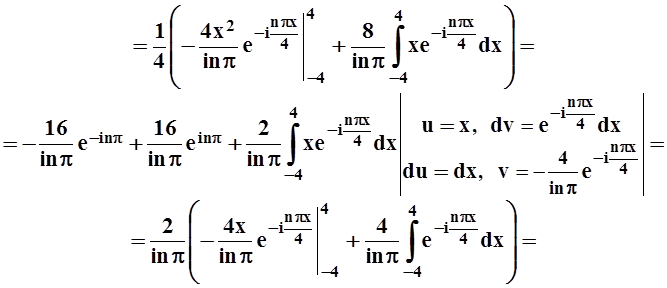
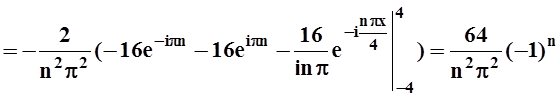 .
.
При n= 0 требуется отдельное вычисление:
c0=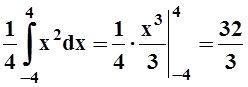 .
.
Получаем, подставляя в общую формулу:
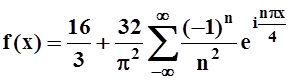 .
.
5.
Представить интегралом Фурье непериодическую функцию 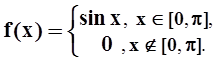
Решение. Ясно, что функция абсолютно интегрируема на всей оси и на любом конечном промежутке разлагается в ряд Фурье (т.е. выполнены условия теоремы Дирихле). Значит, её можно представить интегралом Фурье:
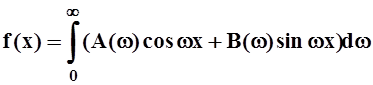 , где
, где 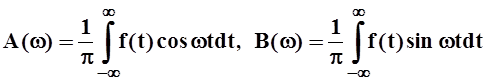 .
.
Так как f(x) не является чётной или нечётной, то придётся вычислять и A(w), и B(w).
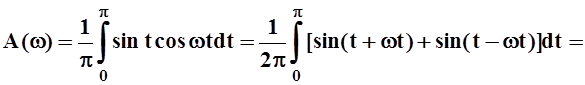
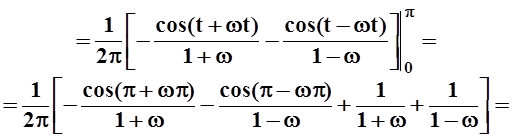
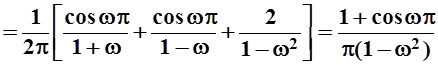 ;
;
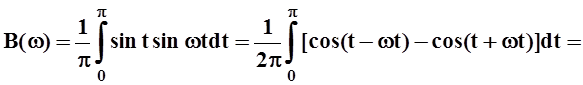
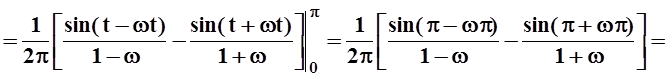
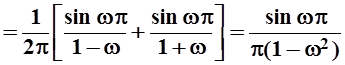 ;
;
Запишем ответ:
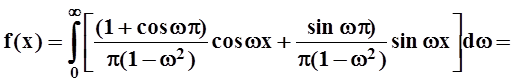
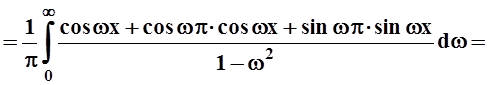
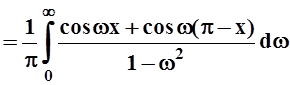 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.