Абстрактные ряды Фурье в гильбертовом пространстве. Интеграл Фурье. Преобразование Фурье, страница 2

В такой записи интеграл Фурье очень похож на ряд Фурье. Частота w здесь изменяется не дискретно (как в случае ряда Фурье), а непрерывно. Поэтому вместо суммы здесь интеграл. Формулы для коэффициентов A(w), B(w) вполне аналогичны формулам для коэффициентов Фурье a_n, b_n.

Наиболее важным, существенным отличием является то, что в ряд Фурье можно разложить лишь периодические функции. В виде интеграла Фурье можно представить и непериодическую функцию.

Пример 5. Представить интегралом Фурье функцию

.

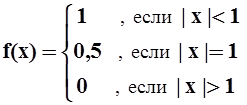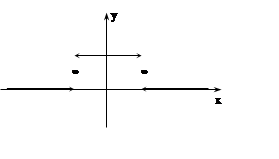
Решение. Построим график f(x). Функция, очевидно, удовлетворяет условиям теоремы 10. Найдём коэффициенты A(w), B(w):

A(w) =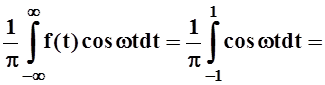

;

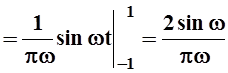B(w) =.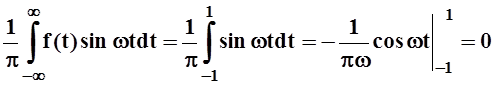

Значит,   f(x) =.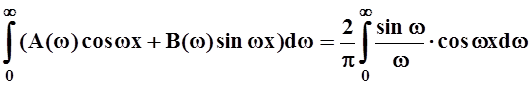

Полученное равенство справедливо и при x= ± 1, так как в данном случае .

Замечание. При x= 0 из выведенной формулы следует, что

.

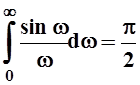Ранее этот интеграл был вычислен другим способом.

Обратим внимание: функция в примере 5 – чётная. Именно поэтому и получилось, что B(w) = 0. Действительно, если f(x) – чётна, то f(x)×sinwx – нечётна, а значит         B(w) =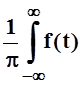sinwtdt= 0.   В этом случае   f(x)×coswx – чётна,  поэтому

A(w) =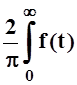cos wt dt.

Аналогично, если  f(x) – нечётная функция, то

A(w) = 0,        B(w) =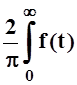sin wt dt.

Если требуется представить интегралом Фурье функцию, определённую на [0, ∞), то можно продолжить её на всю ось так, чтобы она стала чётной (или нечётной, по желанию). Таким образом, функцию, заданную на [0, ∞), можно представить различными интегралами Фурье.

Пример 6. Представить интегралом Фурье функцию   f(x) = e^{– kx}    (k > 0, x ³ 0).

Решение. Если  продолжить f(x) на отрицательную часть действительной оси чётным образом, то получится непрерывная функция. Так мы и поступим. Из-за чётности B(w) = 0. Найдём A(w).

A(w) =.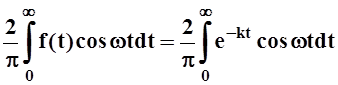

Применим формулу интегрирования по частям. Пусть u= e^–kt, dv= coswtdt. Тогда         du= –ke^–ktdt,  v= sinwt,   и мы получим:

A(w) =.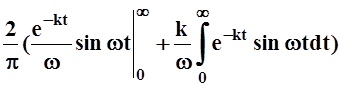

Первое слагаемое, очевидно, равно 0. Второе вычисляем опять с помощью интегрирования по частям:   u= e^–kt,    dv= sinwtdt,   du= –ke^–ktdt,   v= – coswt.        Получим:

A(w) =.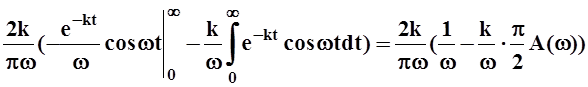

Уравнение относительно  A(w)  легко решается:

.

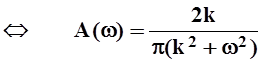Подставляем найденное значение в формулу интеграла Фурье:

f(x) =.

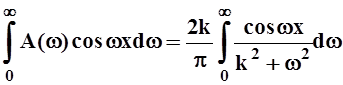Для положительных  x отсюда, в частности, следует:        .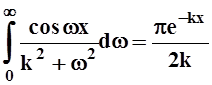

Как и ряд Фурье, интеграл Фурье можно записать в комплексной форме. Так как внутренний интеграл в формуле Фурье

f(x) =

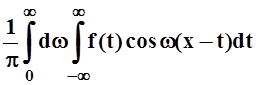
является чётной функцией от w, то можно записать:

f(x) =.

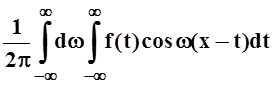Так как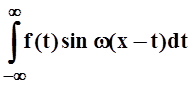 – нечётная функция от  w,  то

0 =.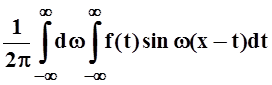

Умножаем последнее равенство на комплексное число i и прибавим к предыдущему. Используя тождество Эйлера:    cosj+isinj= e^ij,  получим:

f(x) =.

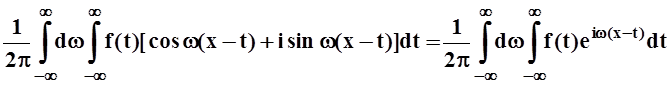Это и есть комплексная форма интеграла Фурье. Проведём в ней дальнейшие преобразования:

f(x) =.

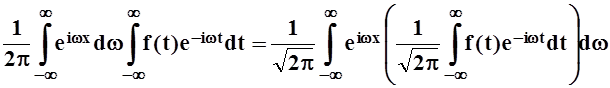Обозначим:

S(w) =.                                               (*)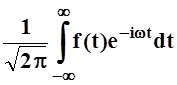

Тогда получим:

f(x) =.                                             (**)

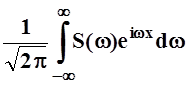Функция S(w) называется преобразованием Фурье функции f(x). Часто преобразованием Фурье называют отображение: f(x) ®S(w), задаваемое формулой (*). Тогда обратное отображение, задаваемое формулой (**), называется обратным преобразованием Фурье.

Комплекснозначная функция S(w), называемая также спектральной плотностью функции f(x), несёт в себе значительную информацию о функции f(x).

Иногда обозначают S(w) = 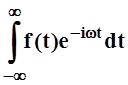. В этом случае обратное преобразование Фурье имеет вид: 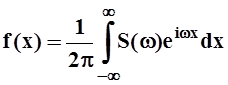.   Мы пользуемся более симметричной записью.

В случае чётной функции f(x) интегральную формулу Фурье можно записать так:

.

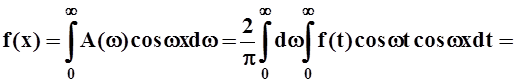
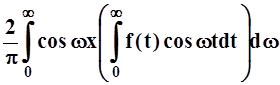Обозначим:

f^*(w) =.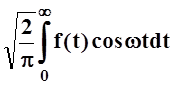

Тогда получим:

f(x) =.

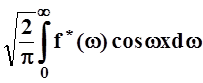Получили две совершенно симметричные формулы. Функция  f^*(w)  называется косинус – преобразованием Фурье функции  f(x).  Ясно, что