Математика \ Вычислительная математика

Приближенное решение уравнений. Отделение корней, страница 4

Метод парабол имеет важное достоинство. Даже если все предыдущие приближения действительны, квадратное уравнение может привести к комплексным числам. Поэтому процесс может сойтись к комплексному корню исходного уравнения.

Пример: Методом парабол найти корень уравнения x3-3x2-13x-7=0 в интервале [-0.8;-0.6] с точностью e =0.0001.

Решение: f(x)=x3-3x2-13x-7, xÎ [-0.8; -0.6]. x0=-0.8; x1=-0.6; x2=-0.7;

f(x0)=0.968; f(x1)=-0.496; f(x2)=0.287.

По точкам x0=-0.8; x1=-0.6; x2=-0.7 построим интерполяционный многочлен второй степени:

P2(x)=f(x2)+(x-x2)× f(x2,x1)+(x-x2)× (x-x1)× f(x2,x1,x0)

P2(x)=0.287+(-7.83)× (x+0.7)+(-5.1)× (x+0.7)× (x+0.6)=-5.1x2-14.46x-7.336

Решая уравнение -5.1x2-14.46x-7.336=0 найдем два корня: x1> -0.66181; x2> -2.17349. В качестве следующего приближения возьмем тот из них, который меньше по модулю, то есть x3> -0.66181

f(x3)=-0.661813-3ћ 0.66181+13ћ 0.66181-7> -0.00032

Построим интерполяционный многочлен второй степени по точкам

x1=-0.6; x2=-0.7; x3=-0.66181:

P2(x)=f(x3)+(x-x3)× f(x3,x2)+(x-x3)× (x-x2)× f(x3,x2,x1)

P2(x)=-0.00032+(-7.52344)× (x+0.66181)+(-4.95972)× (x+0.66181)× (x+0.7)=

=-4.95972x2-14.27764x-7.2770

Решая уравнение -4.95972x2-14.27764x-7.2770=0 найдем два корня:

x1> -0.66185; x2> -2.21687. В качестве следующего приближения возьмем тот из них, который меньше по модулю, то есть x4> -0.66185. Это значение можно взять в качестве приближенного корня уравнения.

п.8. Метод итераций. (Метод повторных подстановок.)

Метод итераций является общим методом решения уравнений. Его применение требует предварительного приведения уравнения к каноническому виду

(13)

Область изменения аргумента x на числовой оси обозначим X. Область значений функции y=j (x) обозначим Y. Функцию j можно рассматривать как оператор, преобразующий X в Y. Уравнение (13) говорит о том, что нужно найти такие точки области X, которые при преобразовании оператором j переходят в себя. Построим график обеих частей уравнения (13). Для левой части это будет прямая y=x. Для правой - некоторая линия y=j (x), которую мы обозначим l.

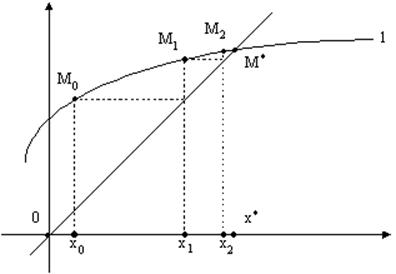
Решением уравнения является абсцисса x* точки M* пересечения l и прямой y=x. Точек M* может быть несколько.

Пусть нам известно какое-либо начальное приближение x0. Все дальнейшие приближения строятся по формуле

(14)

Этот процесс называется простой одношаговой итерацией.

Теорема. Для того, чтобы последовательность приближений x0,x1,? ,xn сходилась к точному решению уравнения x*, необходимо, чтобы для всех xÎ [a,b] выполнялось условие

(15)

Замечание: Привести уравнение к виду (13) можно следующим образом: x=x+c× f(x), где c - произвольная постоянная, которая выбирается так, чтобы для функции j (x)=x+c× f(x) выполнялось условие теоремы.

Пример: Методом итераций найти корень уравнения x3-3x2-13x-7=0 в интервале [-0.8;-0.6] с точностью e =0.0001.

Решение: f(x)=x3-3x2-13x-7, xÎ [-0.8; -0.6].

Приведем уравнение к виду x=j (x): .

Так как , , то условие теоремы выполняется и процесс сходится.

x0=-0.8

x3> -0.67331

x4> -0.66656

x5> -0.66377

x6> -0.66279

x7> -0.66223

x8> -0.66201

x9> -0.66192

x10> -0.66188

x11> -0.66186

Замечание: Для корня из интервала [5.4;5.6] предыдущей формулой пользоваться нельзя, так как . В этом случае данное уравнение можно представить в другом виде, например, x3=3x2+13x+7 и .

Скачать файл