Приближенное решение уравнений. Отделение корней, страница 3

Пример: Методом касательных найти корень уравнения x³-3x²-13x-7=0 в интервале [-0.8;-0.6] с точностью e =0.0001.

Решение: f(x)=x³-3x²-13x-7, xÎ [-0.8; -0.6]. В этом интервале , (случай II), поэтому x₀=b=-0.6. .

f(-0.6)=-0.496; ;

; f(x₁)=-0.01724;

;

; f(x₂)=-0.00001;

x^*> -0.66185

п.5. Комбинированный метод.

Комбинированный метод состоит в совместном использовании метода касательных и метода хорд. Интервал изоляции [a, b] заменяется более узким интервалом изоляции [x₁^х,x₁^к], где x₁^х - абсцисса точки пересечения с осью Ox хорды AB, x₁^к - абсцисса точки пересечения с осью Ox касательной к дуге AB. При этом получим два приближенных значения x₁^х,x₁^к, между которыми содержится искомый корень x^*, то есть "недостаточное" и "избыточное" приближения корня.

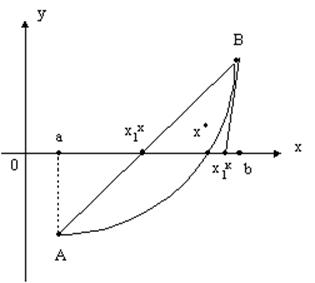
Далее на изоляции корня [x₁^х,x₁^к] применяем метод хорд и метод касательных. Процесс продолжаем до тех пор, пока разность между найденными x_k^х и x_k^к не станет меньше, чем требуемая точность.

По окончании процесса лучше взять (x_k^х+x_k^к).

Пример: Комбинированным методом найти корень уравнения

x³-3x²-13x-7=0 в интервале [-0.8;-0.6] с точностью e =0.0001.

Решение: f(x)=x³-3x²-13x-7, xÎ [-0.8; -0.6]. В этом интервале , (случай II).

x₁^х=-0.66776; f(x₁^х)=0.04541; x₁^к=-0.65962; f(x₁^к)=-0.01724

f(x₂^х)=-0.66186³-3ћ 0.66186+13ћ 0.66186-7> 0.00007

x₂^к=-0.66185; f(x₂^к)=-0.00001

п.6. Метод секущих.

В методе Ньютона требуется вычислять производную функции, что не всегда удобно. Можно заменить производную первой разделенной разностью, найденной по двум последним итерациям, то есть заменить касательную секущей. Тогда вместо формулы (11) получим: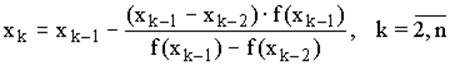(12)

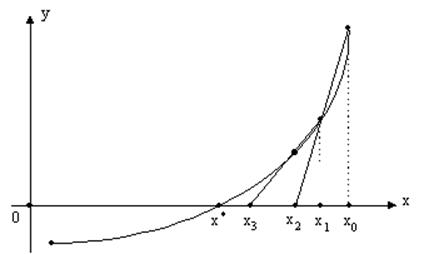
Для начала процесса надо знать x₀ и x₁. Такие процессы, где для вычисления очередного приближения надо знать два предыдущих, называются двухшаговыми.

В знаменателе формулы (12) стоит разность значений функции. Вдали от корня это несущественно, но вблизи корня, значения функции малы и очень близки. Возникает потеря значащих цифр. Это ограничивает точность, с которой можно найти корень.

Пример: Методом секущих найти корень уравнения x³-3x²-13x-7=0 в интервале [-0.8;-0.6] с точностью e =0.0001.

Решение: f(x)=x³-3x²-13x-7, xÎ [-0.8; -0.6]. В этом интервале , (случай II). x₀=b=-0.6; x₁=x₁^к=-0.65962; f(x₀)=-0.496; f(x₁)=-0.01724.

f(x₂)=-0.66177³-3ћ 0.66177+13ћ 0.66177-7> -0.00063

f(x₃)=-0.66185³-3ћ 0.66185+13ћ 0.66185-7> -0.00001

x^*> -0.66185

п.7. Метод парабол.

Метод секущих можно рассматривать как замену функции f(x) интерполяционным многочленом первой степени, проведенным по узлам x_n-1, x_n-2. По трем итерациям можно построить интерполяционный многочлен второй степени, то есть заменить график функции параболой. Запишем интерполяционный многочлен в форме Ньютона

P₂(x)=f(x_n-1)+(x-x_n-1)× f(x_n-1,x_n-2)+ (x-x_n-1)× (x-x_n-2)× f(x_n-1,x_n-2,x_n-3)

Приравнивая его нулю, получим квадратное уравнение. Тот из двух корней, который меньше по модулю, определяет новое приближение x_n=x. Очевидно, для начала расчета надо знать три первых приближения x₀,x₁,x₂, то есть процесс является трехшаговым.

Метод парабол построен по образцу методов третьего порядка. Однако замена производных разделенными разностями приводит к существенному уменьшению скорости сходимости.