¨ bstoer – экстраполяционный метод Булирша-Штера;
¨ polyextr – экстраполяция полиномами;
Ø mgear, lsode – библиотека многошаговых методов для жестских систем;
Выбранный метод указывается после имени библиотеки в квадратных скобках.
· величину абсолютной погрешности решения – abserr = aerr;
· минимальную величину – погрешности minerr = mine.
Глава 3
Решение:
Задание 1.
На сетке [2, 5] найти решение системы двух обыкновенных дифференциальных уравнений 1 порядка
![]() y1’=1/(3+exp(-y1))
y1’=1/(3+exp(-y1))
y2’=1/(2+exp(-y1))
c начальными условиями у1(2)=0 и у2(2)=-3
1. Решение средствами системы Mathcad.
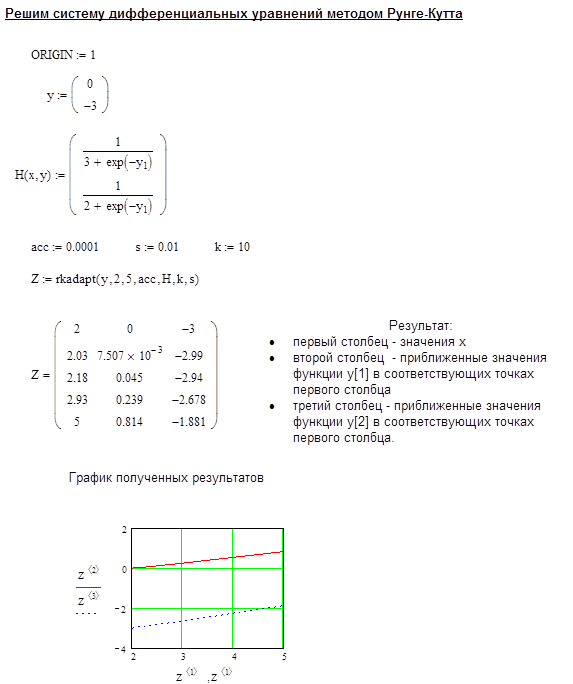

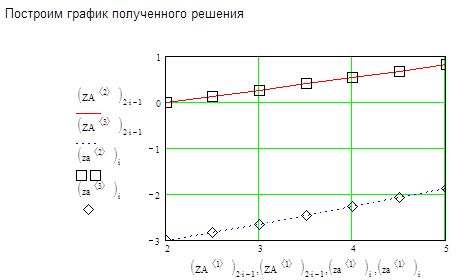
 |

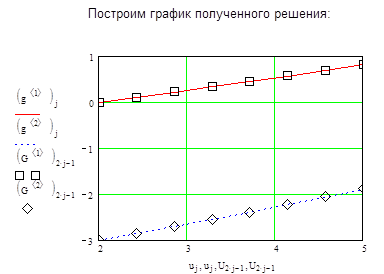
2.Решение средствами Maple.
Зададим уравнения системы и объединим их в систему:
> first:=diff(y1(x),x)=1/(3+exp(-y1));
![]()
> second:=diff(y2(x),x)=1/(2+exp(-y1));
![]()
> deqns:=first,second;
![]()
Зададим список зависимых переменных:
> vars:={y1(x),y2(x)};
![]()
Зададим начальные условия:
> inits:=y1(2)=0,y2(2)=-3;
![]()
Решим систему методом Рунге-Кутта.
> rk:=dsolve({deqns,inits},vars,type=numeric) ;
![]()
> for _e from 2 to 5 by 0.1 do rk(_e); end do;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Построим график полученного решения:
> with(plots):
> s1:=odeplot(rk,[x,y1(x)],2..5,thickness=6):
> s2:=odeplot(rk,[x,y2(x)],2..5,thickness=6):
> display(s1,s2);
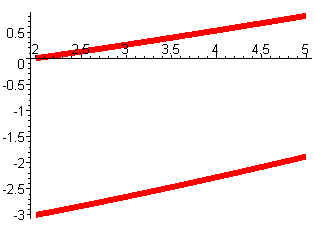
Решим систему методом Булирша-Штера.
>bs:=dsolve({deqns,inits},vars,numeric,method=gear[bstoer]);
![]()
> for _v from 2 to 5 by 1/4 do bs(_v); end do;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Построим график полученного решения:
> s3:=odeplot(bs,[x,y1(x)],2..5,thickness=6):
> s4:=odeplot(bs,[x,y2(x)],2..5,thickness=6):
> display(s3,s4);
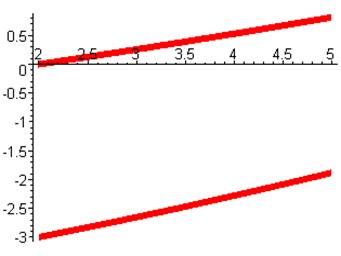
Решим систему методом Эйлера с помощью рекуррентных формул:
> n:=7:a:=2:b:=5:h:=3/7;
![]()
> F1:=(t,w1,w2)->1/(3+exp(-w1));F2:=(t,w1,w2)->1/(2+exp(-w1));
![]()
![]()
> u:=array(1..n+1);u[1]:=2;for j to n do u[j+1]:=u[j]+h od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
столбец u- значения аргумента х.
> g:=array(1..n+1,1..2):g[1,1]:=0; g[1,2]:=-3;for j to n do g[j+1,1]:=evalf(g[j,1]+h*F1(u[j],g[j,1],g[j,2])); g[j+1,2]:=evalf(g[j,2]+h*F2(u[j],g[j,1],g[j,2])) od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Первый столбец в g - примерное значение функции y1(x) в соответствующих точках столбца u, второй столбец- значения функции y2(x).
Для нахождения погрешности найдем решение с меньшим шагом.
> H:=h/2;
![]()
> F1:=(t,w1,w2)->1/(3+exp(-w1));F2:=(t,w1,w2)->1/(2+exp(-w1));
![]()
![]()
> U:=array(1..2*n+2): U[1]:=2; for J to 2*n do U[J+1]:=U[J]+H od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> G:=array(1..2*n+2,1..2): G[1,1]:=0; G[1,2]:=-3;for J to 2*n do G[J+1,1]:=evalf(G[J,1]+H*F1(U[J],G[J,1],G[J,2])); G[J+1,2]:=evalf(G[J,2]+H*F2(U[J],G[J,1],G[J,2])) od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Для построения необходимо сформировать новый массив:
> with(linalg):
> o1:=concat(u,col(g,1)):o1:=convert(o1,listlist):
> o2:=concat(u,col(g,2)):o2:=convert(o2,listlist):
> with(plots):
> s5:=plot([o1,o2]):
> display(s5,thickness=6,color=red);
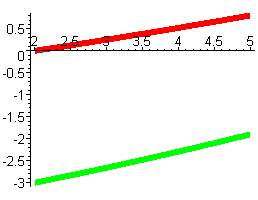
Найдем погрешность для метода Эйлера по правилу Рунге.
> RP:=array(1..n+1,1..2):for j to n+1 do RP[j,1]:=abs(g[j,1]-G[2*j-1,1]); RP[j,2]:=abs(g[j,2]-G[2*j-1,2]) od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> max1:=0;
![]()
> for j to 8 do max1:=max(max1,RP[j,1]) od: print(max1);
![]()
Погрешность для у1(х) равна 0.0046621864
> max2:=0;
![]()
> for j to 8 do if RP[j,2]>max2 then max2:=RP[j,2] fi od; print(max2);
![]()
Погрешность для у2(х) равна 0.008734883
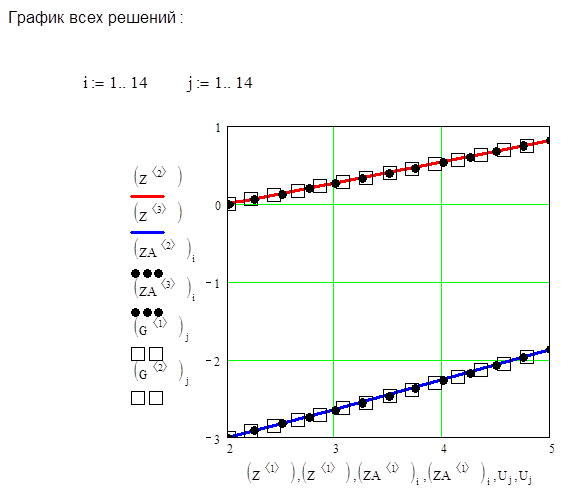
Построим графическое решение для всех трех методов.
> with(plots):
> e1:=odeplot(v,[x,y1(x)],2..5,color=black,thickness=5):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.