Основы математического аппарата и математические модели линейных ДСАУ. Решетчатые функции, страница 4

.        (12.1.)

Пример 1. Записать в развернутой форме выражения для.

Пользуясь формулой (12.1.) и вычислив коэффициенты С₄^ν , получим:

.

.

Сопоставив полученные два выражения нетрудно заметить их подобие и отличия, отмеченные ранее.

1.3. Суммы решётчатых функций

Суммы РФ являются аналогами интегралов. Различают полную и неполную суммы, которые определяются следующим образом:

f_C[n,ε]=Σ_ν=0(n-1)f[ν,ε] неполная сумма (суммируются слагаемые от "0" - го до "(n–1)" - го);

f_C[n,ε]=Σ_ν=0..nf[ν,ε] полная сумма (суммируются слагаемые от "0" - го до "n" - го).⁴⁾

1.4 Разностные уравнения

Представим замкнутую систему со структурой, изображенной на рис 2.1. Она имеет на входе устройство "выборки информации" (квантователь) - идеальный импульсный элемент (ИИЭ) и непрерывную линейную часть (ЛСАУ). На выходе включен второй, но фиктивный квантователь. Поэтому он изображен пунктиром. Оба ИИЭ работают синхронно с периодом квантования Т. На выходе ДСАУ с сигналом ,  может быть включен элемент относительной временной задержкиε (со смещением ε) для второго фиктивного квантователя, чтобы получить дискретный сигнал y[n, ε].

y[n,0]

 

Рис 2.1.

Запишем разностные уравнения для модели такой системы, предполагая, что она имеет порядок "m".

а_mΔ^my[n]+а_m–1Δ^m–1y[n]+...+a₀y[n]=b_kΔ^ke[n]+b_k–1Δ^k–1e[n]+...+b₀e[n].       (14.1.)

Мы получили разностное неоднородное уравнение (РУ) "m" - го порядка. Оно отражает (моделирует) переходные процессы в дискретной  САУ. Здесь возмущением (сигналом управления) является ошибка замкнутой системы e[n] (см. рис 2.1). Если коэффициенты {а_i} и {b_j} постоянны, то выражение (14.1) будет неоднородным линейным разностным уравнением. Оно описывает процессы в линейной дискретной САУ. Для упрощения записи уравнений символом y[n] здесь, и в дальнейшем, обозначены несмещённые y[n, 0] и смещённые y[n, ε] значения решётчатых функций выхода ДСАУ, а  -e[n] -  несмещённая РФ сигнала ошибки e[n, 0]. Только в случае необходимости будет использована более корректная символика для записи РФ.

Как уже говорилось, более удобно работать не с прямыми, а с обратными разностями. Это связано с тем, что для разрешения (14.1.) необходимо знать все последующие значения функций y[0], а именно, y[1], y[2],        y[m-1]и для сигналауправления e [0], соответственно, e [1], e [2],        e [k-1]. Выполнить такие расчеты возможно, но сложно

_________________________________________________________________

⁴⁾ Примечание 4. Рассмотрим интеграл вида:

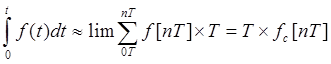.                                                                       (13.1.)

Здесь принято: . Следовательно, при сохранении пределов итегрирования( 0 - t )и уменьшении Т до нуля  число интервалов "n"возрастает до бесконечности.. Поэтому справедлива неопределенность  и такая запись:

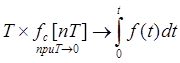
Поэтому составимуравнение, подобное (14.1), но оперируя обратными разностями, в таком виде:

а_mÑ^my[n]+а_m–1Ñ^m–1y[n]+...+a₀y[n]=b_kÑ^ke[n]+b_k–1Ñ^k–1e[n]+...+b₀e[n].       (15.1.)

Для разрешения (15.1.) следует знать предыдущие значения y[0], а именное y[-1], y[-2],   y[-(m-1)]и для сигналауправления e [0], соответственно e [-1], e [-2],        e [-(k-1)], что вполне возможно, особенно при "нулевых" начальных условиях. Сначала перепишем это уравнение, воспользовавшись формами представления разностей высоких порядков (12.1.) с помощью решётчатых функций. Тогда изменятся значения коэффициентов {а_i} и {b_j} и они приобретут вид {с_i} и {d_j}. Расчет численных значений последних выполняется по формулам (17.1.), которые мы приводим и используем без доказательств их достоверности ⁵⁾

Для уравнения (14.1.), где оперируют с прямыми разностями, имеем:

                                           (16.1.)

Для уравнения (15.1.), где оперируют с обратными разностями, найдем:

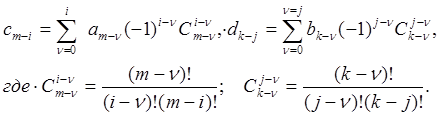                                            (17.1.)

Тогда, например, для уравнения (15.1.) получим

c_my[n]+c_m–1y[n–1]+...+c₀y[n–m]=d_ke[n]+d_k–1e[n–1]+...+d₀e[n–k].(18.1)