Методы линеаризации нелинейностей и нелинейных систем. Линеаризация касательными. Статистическая линеаризация статических и динамических нелинейностей, страница 5

Учтем важное для дальнейших исследований условие. Если структура модели ЛЧ соответствует гипотезе фильтра, то можно считать y(t) моногармонической функцией. Поэтому для реакции НЭ x₂(t) = z(t) так же ограничимся  только одной первой гармоникой (потому как гармоники более высокого порядка через линейную часть не пройдут, и в силу принципа линейности и суперпозиции ЛЧ на выходную координату влияния не окажут). Тогда получим:

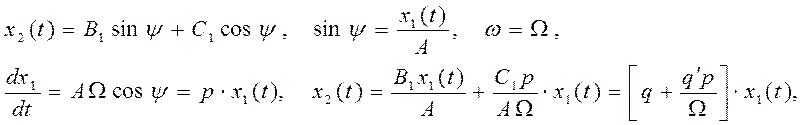
где  и - функции амплитуды входного гармонического сигнала. Как будет показано ниже на конкретных примерах эти коэффициенты  и , и, следовательно,    и   для статических нелинейностей не зависят от частоты входного сигнала.

Итак, имеем: 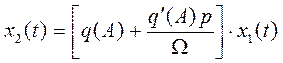.  Можно определить и передаточную функцию эквивалентного линейного элемента:      .                       

Теперь с учетом приведенных выше формул получим:

,    .                                               

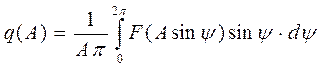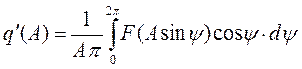Равенством  подчеркнули, что изучаются моногармонические колебательные режимы в НСАУ при гармонически линеаризованной нелинейности.                                                        

По полученной эквивалентной передаточной функции НЭ определим частотные функции НЭ, заменяя в передаточной функции  оператор s  на  jω.

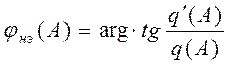, где - амплитудная  характеристика НЭ,

 - фазовая характеристика НЭ.

Из полученных выражений следует, что АФЧХ звена есть не что иное, как комплексный оператор передачи НЭ:   .

Кроме того, амплитудная и фазовая характеристики НЭ не зависят от частоты сигнала, следовательно, не являются частотными характеристиками!!! 

Будем называть такие характеристики динамическими.

Пример 1. Имеется нечетно симметричная однозначная нелинейность (идеальное реле с зоной нечувствительности). На её входе действует гармонический сигнал . Для текущего значения  t   имеем , . Зависимость  построена на правом верхнем рисунке (см. ниже).

Величину  q(A) определим по найденных выше выражениям, пользуясь  графиком. При изменении угла ψ от нуля до значения ψ₁  функция F(Asinψ) = 0, поэтому интеграл вычисляют только на участке от (ψ = ψ₁) до (ψ =) и подобных ему, где функция F(Asin ψ) =. Учтем, что таких участка четыре. Тогда получим:

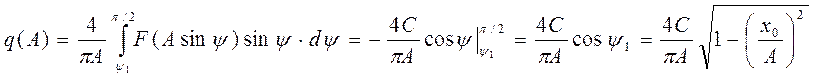, так как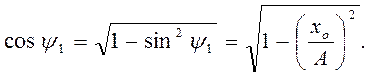  

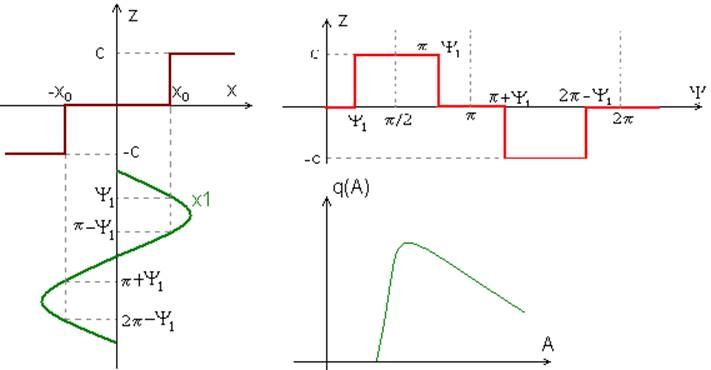
График функции q(A) изображен правом нижнем рисунке.

Так же вычисляется и q^!(A). Но в результате вычислений получим q^!(A)=0.

Вычислять постоянную составляющую x₂₀ не нужно, так её нет на графике функции.

Пример 2. Рассмотрим полиномиальную кубическую однозначную нелинейность .

Зависимость z(-x) = -z(x) – симметричная нечетная. При гармоническом входном сигнале  выходной сигнал может быть описан выражением: +. Тогда, выполняя интегрирование, получаем: =,

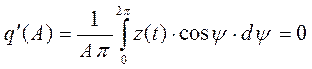. Аналогично предыдущему примеру оба коэффициенты не зависят от частоты ω входного сигнала и .

Теоретически и практически важный вывод. Для однозначных нечетно-симметричных статических нелинейностей коэффициент  всегда равен нулю. Поэтому каждый раз его можно не вычислять.

Коэффициенты гармонической линеаризации двузначных нелинейностей

1. При вычислении коэффициентов гармонической линеаризации двузначных нелинейностей можно предполагать, что они будут различными для опережающих и отстающих нелинейностей.

2. Поскольку контур обхода нелинейности при возрастании x₁ и уменьшении x₁ будут разными, то коэффициент  не будет иметь нулевого значения.

3. Площадь петли гистерезиса нелинейностей будет влиять на характер динамических процессов в линеаризированных таким способом НСАУ.

При вычислении  можно сказать, что . Тогда   , откуда  . В итоге получаем: , где s - площадь петли, s=4bc.

Если гистерезис отстающий (как  показано на рисунке), то площадь петли берут со знаком минус, при опережающем гистерезисе в полученной формуле будет стоять знак плюс.

Для рассматриваемой нелинейности коэффициент . Оператор передачи данной двузначной нелинейности будет иметь вид: , при этом  комплексный коэффициент передачи нелинейности: .

Комплексный коэффициент передачи динамической  нелинейности

Динамическая нелинейность характеризуется выражением: F(x, px). Поскольку , а , то коэффициент q(A,Ω)- функция амплитуды и частоты. Аналогично и q`(A, Ω).